P and SV waves

In a transversely isotropic medium, the phase velocity $v(\theta)$ for P and SV waves is expressed as follows (Auld, 1990):

$$\begin{eqnarray} 2 \rho v^2 (\theta) & = & c_{11} \sin^2 (\theta) + c_{33} \cos^... ...^2 (\theta)]^2 + (c_{13} + c_{44})^2 \sin^2 (2 \theta)}, \nonumber\end{eqnarray}$$ (7)

where c_ij are four of the five elastic constants that describe an homogeneous transversely isotropic medium. The sing ``+'' in front of the square root corresponds to P waves and the ``-'' to SV waves.

An equation for the transmitted phase angle $\theta_t$ as a function of the incident p can be obtained after substituting equation (7) into equation (5), resulting the following fourth order polynomial in $\tan (\theta_t)$:

$$a_0 + a_1 \tan(\theta_t) + a_2 \tan^2 (\theta_t) + a_3 \tan^3 (\theta_t) + a_4 \tan^4 (\theta_t) \ =\ 0,$$ (8)

where the coefficients a_i are given in Appendix A. A similar expression obtained by Byun (1984) is no correct because $\theta_t = - \gamma_2$ is not a root of the polynomial when p = 0, as equation (5) predicts.

As shown in Appendix A, the coefficients a_i are the same for both P and SV waves (the $\pm$ in front of the square root in equation (7) is lost in the derivation of (8)) and they are independent on the sign of p. In principle, by solving this equation at each interface, it should be possible to find the angle of the transmitted phase by computing the arctangent of one of its roots. However, the procedure is not straight forward. In one hand, we have to identify the solutions that correspond to p or -p and P or SV waves. On the other hand, finding an angle from its tangent is not a one to one transformation because $\tan (\theta) = \tan (\theta + n \pi)$ and therefore, infinite angles satisfy equation (8). Besides these problems, we have to deal usually with the difficulties of solving equation (8) numerically.

Let's examine first the numerical problems. It is well known that most algorithms used to find roots of polynomials fail in the presence of multiple (or close to multiple) roots. This is the case of equation (8) when p = 0. From equation (5), we obtained that in this case the transmitted phase angle is $\theta_t = - \gamma_2$and therefore, it is not necessary to solve equation (8) when p=0. Problems may also arise when $p \approx 0$ because the roots are close of being multiple. The way I found around this problem was based on the assumption that the slowness surface is an smooth function of $\theta$ and then, when $p \approx 0$, $v_2(\theta_t) \approx v_2 (-\gamma)$.If this is true, $\theta_{t_0} = - \gamma_2$ can be used as ``starting'' point to find $\theta_t$ by successive applications of equation (5) as follows:

$$\theta_{t_{i+1}} \ =\ \sin^{-1} (p v_2(\theta_{t_i})) - \gamma_2.$$ (9)

Typically, only one iteration is required.

Figure  shows how to solve equation (8) graphically. From the construction with the slowness surfaces, we see that the infinite roots of equation (8) that I mention before correspond to only eight different points in the slowness surfaces for both P and SV waves. In this figure I assume that the incident phase (not shown) is crossing the interface from medium 1 to medium 2. For simplicity, I assume that both media are isotropic. The slowness surfaces in medium 2 are represented one half by continuous circles and the other half by dotted circles. The slowness surfaces in medium 1 are not shown. For a given $\pm p$ value at the interface, this figure shows the position of all the possible points in the P and SV slowness surfaces whose angle measured from the symmetry axis satisfy equation (8). These points are obtained by simple application of the kinematic boundary condition (3). The points A, B, C, and D are the solutions for negative p and the points H, G, F and E are obtained by adding $\pm \pi$ to the previous ones and they are the solutions for positive p. If $\vert p \vert \gt \frac{1}{v_p}$ two of the roots of (8) are complex and the and there are no transmitted P waves. If $\vert p \vert \gt \frac{1}{v_s}$ the four foots are complex and there are no transmitted SV waves either. I will assume that when the transmitted ray travels parallel to the interface, it doesn't go back to the previous medium, which is a simplification of real the behavior of head waves.

 

eight-roots
Figure 4 Graphical solution for the angle of the transmitted phase as a function of the incident p. The the tangent of the angles at A, B, C, D, E, F, G and H are roots of equation (8). Among these eight angles, only one reproduces the incident p for the corresponding wave type in the expected direction. When solving equation (8) numerically, only those angles at $\pm 90$ degrees from the axis of symmetry are obtained. The axes of symmetry 1 and 2 are two of the possible axes of symmetry of the isotropic medium where the transmitted phase travels.

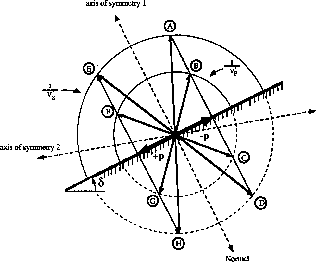When the axis of symmetry and the normal to the interface are parallel (axis of symmetry 1 in Figure ), the arctangent of the roots of equation (8) give the angles of the points A, B, E and F. This is because the FORTRAN function ATAN gives its results in the interval $( - \pi/2 , + \pi/2)$ and this is exactly the domain of the phase angle measured from the axis of symmetry. If we take 2 as the axis of symmetry (which is true here because the medium is isotropic), the roots of equation (8) give the points E, F, G and H. None of this points is the correct one when, for example, a P wave impinges on the interface with negative p. The point B is the solution in this case.

The previous example tells us that when the axis of symmetry and the normal to the interface are not parallel, the roots of equation (8) may not give the expected direction for the refracted phase. For this reason, it is necessary to examine all the eight angles and pick the one that verifies equation (5) for the desired wave type (with this, the number of possible angles is reduced from eight to two) and produces a ray pointing towards the expected direction (which further reduces the number of angles from two to one). This will be explained in more detail in the next section, for SH waves.