SH waves in a transversely isotropic medium have elliptical slowness and wave surfaces. An elliptical slowness surface may not be a good global (ie., for all angles) approximation for a P or SV slowness surface in a transversely isotropic medium, but it is a good paraxial approximation (Dellinger and Muir, 1991). Hence the importance of elliptical anisotropy in data fitting, specially when the measurements have limited aperture, as explain by Dellinger Muir (1991) and Michelena (1992).
Byun (1982) shows that when the slowness surfaces are elliptical
the calculation at each interface of the
refracted ray angle ![]() is simpler, because the phase
angle
is simpler, because the phase
angle ![]() does not need to be explicitly computed. Byun's expression
for the ray parameter as a function of the ray is angle at each interface
is
does not need to be explicitly computed. Byun's expression
for the ray parameter as a function of the ray is angle at each interface
is
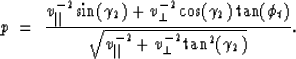 |
(10) |
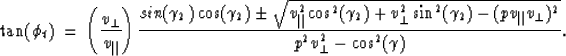 |
(11) |
If we take the extra step of solving explicitly
for the phase angle at each interface,
we have to look among the four different
points in the slowness surface whose
angles satisfy equation (5) and keep the one that
produces a ray pointing in the desired direction.
The ``desired direction'' depends on the type
of problem where the ray tracer is used.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how to pick the roots that correspond to
transmitted rays, the ones needed in transmission
traveltime tomography.
shows how to pick the roots that correspond to
transmitted rays, the ones needed in transmission
traveltime tomography.
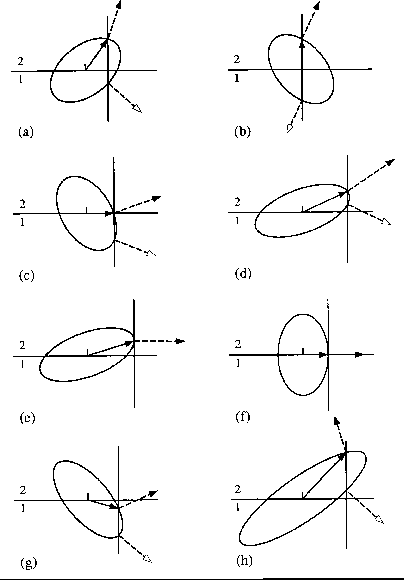 |
In this figure, the horizontal distance from
the center of the each
ellipse to the vertical line is equal to the incident p.
As we see,
to obtain transmitted rays (dashed arrows with black head),
it is enough
to pick the root that produces a ray pointing towards medium 2.
In some cases the transmitted ray can travel parallel to the interface
with the phase direction (continuous arrows) parallel to it or not
(Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -f and
-f and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -e respectively).
The emergent phase angle may be greater than 90 degrees for the
transmitted ray, as shown in Figure
-e respectively).
The emergent phase angle may be greater than 90 degrees for the
transmitted ray, as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -g.
The ray pointing towards medium 2 may also go backwards, as
Figure
-g.
The ray pointing towards medium 2 may also go backwards, as
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -h shows.
When the vertical line doesn't intersects the ellipse, there are
not transmitted but only reflected rays (angle of incidence
greater than the critical angle). However, in order to keep
track more easily of the rays that hit the interface at post-critical
angles, I will assume that those rays continue traveling along the interface.
The inversion procedure I describe in a separate paper (Michelena, 1992)
doesn't use these rays.
-h shows.
When the vertical line doesn't intersects the ellipse, there are
not transmitted but only reflected rays (angle of incidence
greater than the critical angle). However, in order to keep
track more easily of the rays that hit the interface at post-critical
angles, I will assume that those rays continue traveling along the interface.
The inversion procedure I describe in a separate paper (Michelena, 1992)
doesn't use these rays.