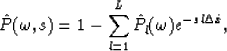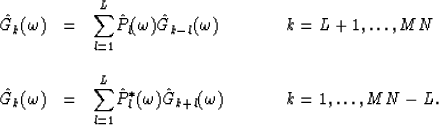Next: Spitz's stretching method
Up: THE LINEAR TWO-STEP METHOD
Previous: Linear events
The events on a real seismic section are generally not linear events,
but their trajectories can be approximated by piecewise lines.
Therefore, if we divide the section into many small subsections,
we expect to see only linear events in each of these subsections.
Let 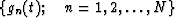 denote N traces that form
a subsection, and suppose that this subsection contains L linear events.
This subsection can be modeled in the time domain as
denote N traces that form
a subsection, and suppose that this subsection contains L linear events.
This subsection can be modeled in the time domain as
| 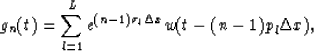 |
(1) |
and in the frequency domain as
| 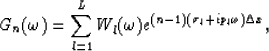 |
(2) |
where 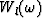 is the
Fourier transform of the wavelet of the lth event
and
is the
Fourier transform of the wavelet of the lth event
and 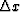 is the spatial
sampling interval. With a proof similar to Canales' (Canales, 1984), we can
show that for each frequency
is the spatial
sampling interval. With a proof similar to Canales' (Canales, 1984), we can
show that for each frequency 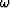 ,
, 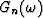 can be
predicted by a one-step linear prediction filter, as follows:
can be
predicted by a one-step linear prediction filter, as follows:
| 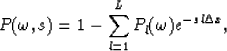 |
(3) |
where 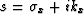 is the generalized complex wave-number.
The coefficients of the filter can be computed from the following linear system:
is the generalized complex wave-number.
The coefficients of the filter can be computed from the following linear system:
| 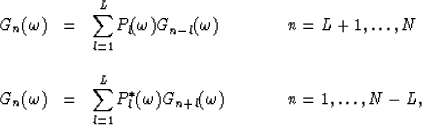 |
(4) |
where  stands for the complex conjugate. If we interpolate
(M-1) traces between each pair of known traces, the output section should be
stands for the complex conjugate. If we interpolate
(M-1) traces between each pair of known traces, the output section should be
| 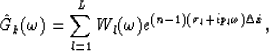 |
(5) |
where 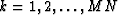 , and
, and
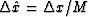 is the new spatial sampling interval
after trace interpolation.
is the new spatial sampling interval
after trace interpolation.
Like 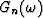 ,
, 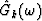 can be predicted by a prediction
filter, as follows:
can be predicted by a prediction
filter, as follows:
| 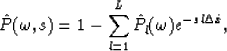 |
(6) |
whose coefficients similarly satisfy the linear system as follows:
| 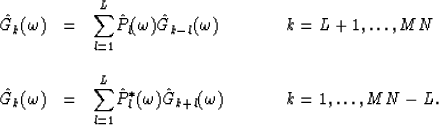 |
(7) |
Since the interpolation process should not change the known traces, we have
| 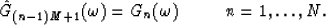 |
(8) |
For each 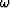 , equations (7) and (8)
define a constrained linear system whose solution determines the missing
traces.
, equations (7) and (8)
define a constrained linear system whose solution determines the missing
traces.





Next: Spitz's stretching method
Up: THE LINEAR TWO-STEP METHOD
Previous: Linear events
Stanford Exploration Project
11/18/1997
![]() denote N traces that form
a subsection, and suppose that this subsection contains L linear events.
This subsection can be modeled in the time domain as
denote N traces that form
a subsection, and suppose that this subsection contains L linear events.
This subsection can be modeled in the time domain as
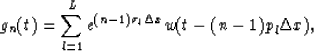
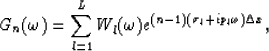
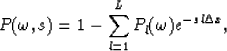
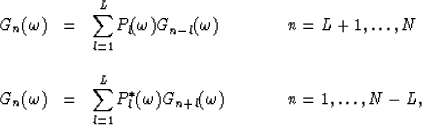
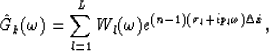
![]() ,
, ![]() can be predicted by a prediction
filter, as follows:
can be predicted by a prediction
filter, as follows: