Iterative velocity transform

After we use data to determine a velocity model (or slowness model) with an operator $\bold A$we may wonder whether synthetic data made from that model with the conjugate operator $\bold A'$ resembles the original data. In other words, we may wonder how close the velocity transform $\bold A$comes to being unitary. The first time I tried this, I discovered that large offsets and large slownesses were attenuated. With a bit of experimentation I found that the scale factor $\sqrt{sx}$seems to make the velocity transform approximately a unitary one. Results are in Figure 16.

 

aavel1
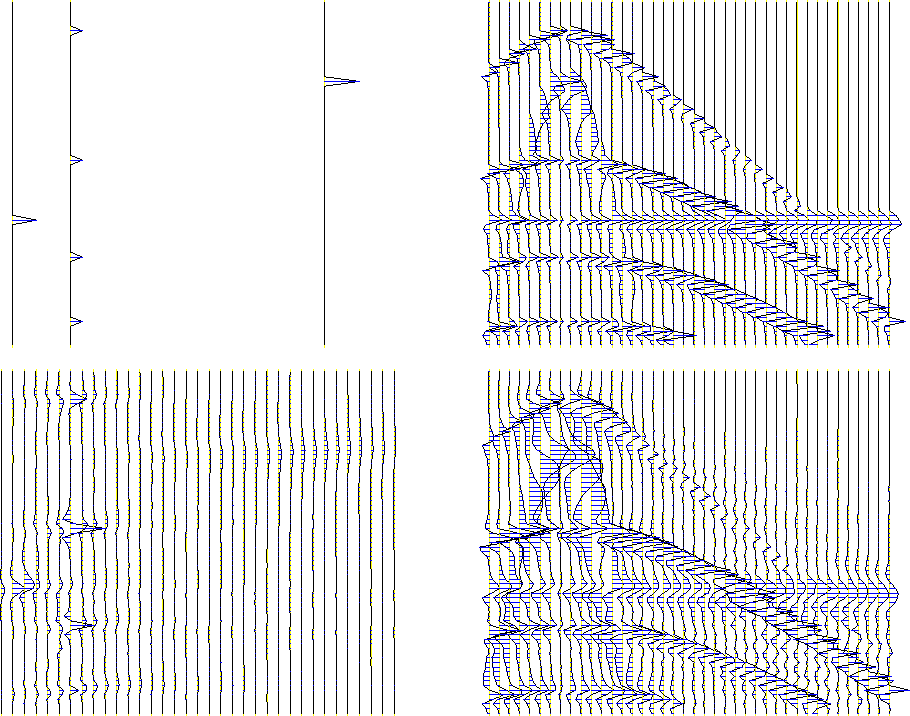
Figure 16 Top left: Slowness model. Top right: Data derived from it using the pseudounitary scale factor. Bottom left: the velocity spectrum of top right. Bottom right: data made from velocity spectrum.

Figure 16 shows that on a second pass, the velocity spectrum of the slow wave is much smoothed. This suggests that it might be more efficient to parameterize the data with slowness squared rather than slowness itself. Another interesting thing about using slowness squared as an independent variable is that when slowness squared is negative (velocity imaginary) the data is matched by ellipses curving up instead of of hyperbolas curving down.

 

aavel0
Figure 17 Like Figure 16 but with antialias=0. This synthetic data presumes no receiver groups in the field recording.

Figure 17 shows the effect of no antialiasing in either the field recording or the processing. The velocity spectrum is as sharp, if not sharper, but it is marred by a large amount of low-level noise.

Aliased data gives an interesting question. Should we use an aliased operator as in Figure 17 or should we use an antialiased operator as that in Figure 16? Figure 18 shows the resulting velocity analysis. The antialiased operator seems well worth while, even when applied to aliased data.

 

adataavel Figure 18 Aliased data analyzed with antialiased operator. Compare to the lower left of Figure 17.

In real life, the field arrays are not ``dynamic'' (able to respond with space and time variable s₀) but the data processing can be dynamic. Fourier and finite-difference methods of wave propagation and data processing are generally immune to aliasing difficulties. On the other hand, dynamic arrays in the data processing are a helpful feature of the ray approach whose counterparts seem unknown with Fourier and finite-difference techniques.

Since $\sqrt{sx}$ does not appear in physical modeling, people are sometimes hesitant to put it in the velocity analysis. If $\sqrt{sx}$ is omitted from the modeling, then |sx| should be put in the velocity analysis. Failing to do so will give a result like in figure 19. The principal feature of such a velocity analysis is the velocity smearing. A reason for smearing is that the zero-offset signal is strong in all velocities. Multiplying by $\sqrt{sx}$ kills that signal (which is never recorded in the field anyway). The conceptual advantage of a pseudounitary transformation like Figure 16 is that points in velocity space are orthogonal components like Fourier components whereas for nonunitary transforms like with Figure 19 the different points in velocity space are not orthogonal components.

 

velsmear
Figure 19 Like Figure 16 omitting pseudounitary scaling. psun=0. Right is synthetic data and left the analysis of it which is badly smeared.

Subroutine veltran() does the work.

# veltran -- velocity transform with anti-aliasing and sqrt(-i omega)
#
subroutine veltran(conj,add,psun,s02,anti,t0,dt,x0,dx,s0,ds,nt,nx,ns,model,data)
integer it,ix,is,  conj,add,psun,                           nt,nx,ns
real x, s, wt,               s02,anti,t0,dt,x0,dx,s0,ds,model(nt,ns),data(nt,nx)
temporary real slow(nt), half(nt,nx)
call null(               half,nt*nx)
call conjnull(     conj,add,                            model,nt*ns, data,nt*nx)
if( conj != 0)	do ix = 1, nx 
			call halfdifa( conj,   0, nt, half(1, ix), data(1, ix) )
do is= 1, ns {  s = s0 + (is-1) * ds;   do it=1,nt { slow(it) = s}
do ix= 1, nx {  x = x0 + (ix-1) * dx
	if     ( psun == 2 ) {  wt =       abs( s * x)  }	# vel tran
	else if( psun == 1 ) {  wt = sqrt( abs( s * x)) }	# pseudounitary
	else	             {  wt = 1.                 }	# modeling
	call trimo( conj, 1, t0,dt,dx, x, nt,slow, s02,
			wt , anti,  model(1,is),  half(1,ix))
	}}
if( conj == 0)	do ix = 1, nx 
			call halfdifa( conj, add, nt, half(1, ix), data(1, ix) )
return; end