CODING NMO WITH RECTANGLES

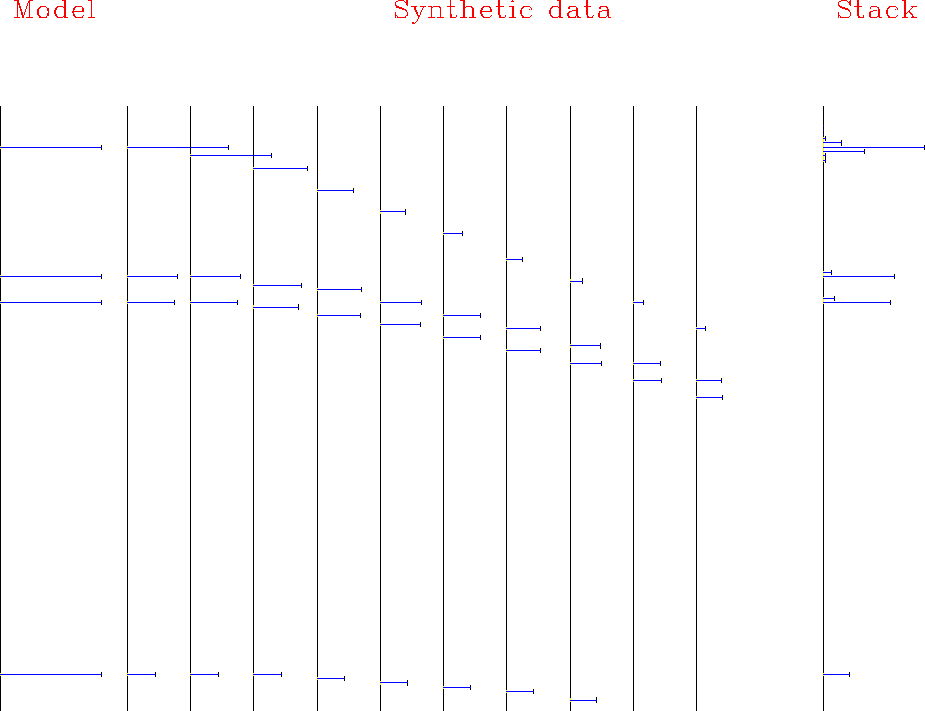A subroutine for causal summation is causint().

# causal integral
#
subroutine causint(  conj, add,        n,pp,  qq   )
integer i,        n, conj, add;   real pp(n), qq(n )
temporary real tt(n)
call conjnull(       conj, add,        pp,n,  qq,n )
if( conj == 0 ) {			tt(1) = pp(1)
					do i= 2, n
						tt(i) = tt(i-1) + pp(i)
					do i= 1, n
						qq(i) = qq(i) + tt(i)
					}
else {		tt(n) = qq(n)
		do i= n, 2, -1 
			tt(i-1) = tt(i) + qq(i-1)
		do i= 1, n
			pp(i) = pp(i) + tt(i)
		}
return; end

The conjugate of causal integration is anticausal integration. (See PVI Claerbout (1992) for fuller explanation of conjugates and this detail.) For each reflector, data modeling proceeds by throwing out two pulses of opposite polarity. Then causal summation produces a rectangle (also called ``box car'') between the pulses. When moving out data, anticausal summation is the first step. Thus each impulse in the data becomes a rectangle from the impulse to t=0. Then subtracting values at rectangle ends gives the desired integral of data in the rectangle. The code is in subroutines boxmo() and boxstack(). The travel-time depth $\tau$ is denoted by z in the code. The inverse of the earth velocity $v(\tau)$,called the slowness $s(\tau )$, is denoted by slow(iz).

subroutine boxstack( conj,add,slow,antialias, t0,dt,x0,dx,nt,nx, stack, gather)
integer conj, add, ix, nx, nt
real x,                slow(nt),antialias, t0,dt,x0,dx, stack(nt), gather(nt,nx)
call conjnull( conj, add, stack, nt, gather, nt*nx)
do ix= 1, nx {	x =  x0 + dx * (ix-1)
	call boxmo(conj,1,t0,dt,dx,x,nt,slow,antialias, stack, gather(1,ix))
	}
return; end

subroutine boxmo( conj, add, t0,dt, dx, x, nt,slow,  antialias, zz,     tt   )
integer it,iz,itp,conj, add,               nt
real t, tp, z, amp,          t0,dt, dx, x, slow(nt), antialias, zz(nt), tt(nt)
temporary real ss(nt)
call null(     ss,nt);		call conjnull( conj, add,       zz,nt,  tt,nt)
if( conj != 0)			call causint(     1,   0, nt, ss, tt)
do iz= 1, nt {	z = t0 + dt*(iz-1)
	t = sqrt( z**2 + (slow(iz)* abs(x)         )**2 ); it = 1.5 + (t -t0)/dt
	tp= sqrt( z**2 + (slow(iz)*(abs(x)+abs(dx)))**2 )
	tp = t + antialias * (tp - t) + dt;                itp= 1.5 + (tp-t0)/dt
	amp =  sqrt( nt*dt/(t+dt)) * (z+dt)/(t+dt) / (itp - it)
	if ( itp < nt   ) {
		if( conj == 0 ) {	ss(it ) = ss(it ) + amp * zz(iz)
					ss(itp) = ss(itp) - amp * zz(iz)
					}
		else            {	zz(iz) = zz(iz)  + amp * ss(it )
					zz(iz) = zz(iz)  - amp * ss(itp)
					}
		}
	}
if( conj == 0)		call causint(     0,  add, nt, ss, tt)
return; end

To find the end points of the rectangular intervals, given the vertical travel time, I get the time t, in the usual way. Likewise I get the time, tp, on the next further-out trace for the ending location of the rectangle wavelet. I introduce a parameter called antialias that can be used to increase or decrease the tp-t gap. Normally antialias=1.

Theoretical solutions to various problems lead to various expressions for amplitude along the hyperbola. I set the amplitude amp by a complicated expression that I do not defend or explain fully here but merely indicate that: a ``divergence'' correction is in the factor sqrt( nt*dt/(t+dt)); a cosine like ``obliquity'' scale is z/t; and the wavelet area must be conserved, so the height is inversely proportional to the pulse width (itp - it). Wavelet area is conserved to assure that after low-pass filtering, the strength of a wave is independent of whether it straddled two mesh points as (.5,.5) or lay wholly on one of them as (1,0).

To test a limiting case, I set the antialias parameter to zero and show the result in Figure 5 which is the same as the simple prescription to ``sum over the x-axis.'' We notice that the final stack is not the perfect impulses that we began with. The explanation is: information can be expanded in time and then compressed with no loss, but here it is compressed first and then expanded, so the original location is smeared. Notice also that the full amplitude is not recovered on the latest event. The explanation is that a significant fraction of the angular aperture has been truncated at the widest offset.

 

boxmo0 Figure 5 Rectangles shortened to one point duration. (antialias=0.)