




Next: SOLVING THE FREQUENCY-DEPENDENT EIKONAL
Up: Biondi: Solving the frequency-dependent
Previous: INTRODUCTION
The frequency-dependent eikonal equation can be easily derived
starting from the scalar wave equation:
| 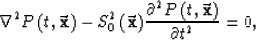 |
(1) |
where 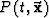 is the wavefield, as a function
of the position
is the wavefield, as a function
of the position 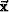 and time t, and
and time t, and 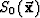 is the
slowness of the medium.
Fourier transforming the time coordinate we get the
Helmholtz equation:
is the
slowness of the medium.
Fourier transforming the time coordinate we get the
Helmholtz equation:
| 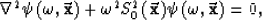 |
(2) |
where 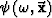 is the transformed wavefield,
and
is the transformed wavefield,
and 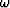 the temporal frequency.
the temporal frequency.
The next step is to substitute into the Helmholtz equation the trial
solution,
| 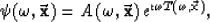 |
(3) |
where 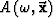 is the amplitude of the wavefield, and
is the amplitude of the wavefield, and
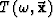 the time delay, or traveltime.
Equating the real part of equation (2)
we get the
frequency-dependent eikonal equation,
Beydoun (1985); Zhu (1988)
the time delay, or traveltime.
Equating the real part of equation (2)
we get the
frequency-dependent eikonal equation,
Beydoun (1985); Zhu (1988)
| 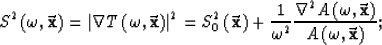 |
(4) |
where 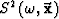 is the phase slowness, that is function of frequency.
Equating the imaginary part of equation (2)
we get the
transport equation
is the phase slowness, that is function of frequency.
Equating the imaginary part of equation (2)
we get the
transport equation
| ![\begin{displaymath}
\nabla \cdot \left[ A^2 \left( \omega,{\bf \vec x}\right)\nabla {T \left( \omega,{\bf \vec x}\right)}\right] =0.\end{displaymath}](img13.gif) |
(5) |
The conventional eikonal equation
is derived by dropping
the second term on the right of equation (4).
The second term can be dropped when
| 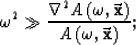 |
(6) |
that is, when
the frequency of the propagating waves is sufficiently
large, with respect to the relative amplitude variations.
In this case, the traveltimes are independent
from the amplitudes, and
the two equations can be solved sequentially.
First, the eikonal is solved for the traveltimes;
second, the amplitudes are computed using the transport equation.
The most common method for computing the amplitudes
is to recognize that
the transport equation
dictates that
the product of the square of the amplitude with
the phase slowness (A2 S)
is preserved along a ray tube.
The amplitude can be thus expressed as
| 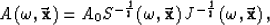 |
(7) |
where A0 is the amplitude at the source
and 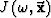 is the Jacobian of mapping via rays
Bleistein (1984).
The amplitude is thus dependent on the phase slowness
is the Jacobian of mapping via rays
Bleistein (1984).
The amplitude is thus dependent on the phase slowness 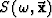 ,and on the Jacobian
,and on the Jacobian 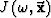 , which is
proportional
to the ray density.
The validity of the condition expressed in (6) is
thus dependent on both the rate of variation of the phase slowness
and on the rate of variation of ray density.
For example, in presence of caustics, the condition in (6)
can be violated even if the phase-slowness function is smooth.
, which is
proportional
to the ray density.
The validity of the condition expressed in (6) is
thus dependent on both the rate of variation of the phase slowness
and on the rate of variation of ray density.
For example, in presence of caustics, the condition in (6)
can be violated even if the phase-slowness function is smooth.





Next: SOLVING THE FREQUENCY-DEPENDENT EIKONAL
Up: Biondi: Solving the frequency-dependent
Previous: INTRODUCTION
Stanford Exploration Project
11/18/1997