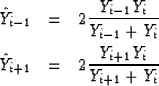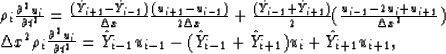Next: The Shoenberg-Muir equivalence
Up: THEORY
Previous: THEORY
Let's consider the 1-D elastic system shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
which can either represent a discrete system or the discrete representation of
a continuous system. Differently from the system in Cunha (1991), this
system represents the masses and springs as a single entity.
In the case of a discrete system, the equation of motion for point i is
,
which can either represent a discrete system or the discrete representation of
a continuous system. Differently from the system in Cunha (1991), this
system represents the masses and springs as a single entity.
In the case of a discrete system, the equation of motion for point i is
| 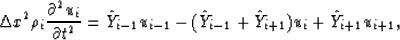 |
(1) |
where
| 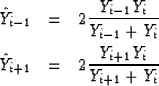 |
|
| (2) |
are the equivalent Young moduli that control the interaction between
adjacent units of the system.
spring2
Figure 1 A mass-spring model that can represent either a discrete physical system
or the discretization of a continuous elastic system.

On the other hand, if we consider the system as continuous, the continuous
equation to be discretized is
| 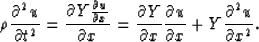 |
(3) |
Two important related issues come up in the discretization of (3):
the definition of the appropriate Y to use in each of the terms of
the equation, and the choice of the differential star for the first-order
derivative. If we choose the more precise (-1,1) star, the two terms
of equation (3) will not be centered at the same point, while the
star (-.5,0,.5) will not have the same resolution.
Looking into the physics of the process gives a clue
for the correct choice of Y; it is the one that is actually involved in the
interaction between adjacent points (the equivalent Young modulus).
It turns out that this choice also solves the problem of the differential star.
Using this criterion, the discretization of (3) leads to
which is identical to equation (1).
Using equation (1) as the basis for the discretization
process offers some advantages over the usual methods.
The differential operator can be applied in a single
stage (without the intermediate evaluation of strain components),
allowing for the design of a more efficient algorithm.
In addition, the differentiation of the model parameters is completely
separated from the differentiation of the wavefield components, and
since the model parameters do not change with time their derivatives
need to be computed only once. This independence of the derivatives of the
elastic constants relative to the wavefield has an extra advantage when
a blocky model (one with sharp boundaries) is to be modeled.
In such models, a short two-point operator can be used for the elastic
derivatives since large operators will not give the right answer at
the boundaries because blocky models are aliased.
Finally, the operation can be implemented in a non-staggered grid, since
it is executed in one stage and all derivatives are centered.





Next: The Shoenberg-Muir equivalence
Up: THEORY
Previous: THEORY
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
which can either represent a discrete system or the discrete representation of
a continuous system. Differently from the system in Cunha (1991), this
system represents the masses and springs as a single entity.
In the case of a discrete system, the equation of motion for point i is
,
which can either represent a discrete system or the discrete representation of
a continuous system. Differently from the system in Cunha (1991), this
system represents the masses and springs as a single entity.
In the case of a discrete system, the equation of motion for point i is