Meaning of the results

Isotropic tomography fits circles (t² = (x² + z²) S²) to the data. Anisotropic tomography fits ellipses (t² = x² S_x² + z² S_z²). Depending on the range of ray angles available (or the geometry used) and the wave type under consideration, the estimated slownesses S_x and S_z may or may not correspond to the real slownesses of the medium.

Horizontal or near horizontal rays are typical of a cross-well geometry. These rays sample a portion of the slowness surface close to the horizontal and for this reason the estimated S_x corresponds to the real horizontal slowness. On the contrary, S_z is not sampled by cross-well geometries. The inversion gives the vertical slowness of the best fitting ellipse (S_znmo) which coincides with the real vertical slowness only if the wave type considered is SH. However, we can generally expect S_znmo to be closer than S to the real vertical slowness. This will be illustrated later with field data by comparing S, S_x and S_znmo with sonic logs.

Vertical or near vertical rays are typical of a VSP-like geometry. From this type of geometry we can get S_xnmo and S_z. These two slownesses plus S_x and S_znmo obtained from cross-well geometries can be used to estimate the real slowness surface of the medium $S( \phi )$using the following approximate expression (Muir, 1990):

$$S( \phi ) \ =\ \frac{M_x^3 c^6 + M_x x^2 (2M_z + M_{znmo})c^... ... M_{xnmo})c^2 s^4 + M_z^3 s^6}{(M_x c^2 + M_z s^2)^2} \nonumber$$

where

$$\begin{eqnarray} M_x & = & S_{x}^{-2} \nonumber \\ M_z & = & S_{z}^{-2} \nonum... ...onumber \\ \phi & = & \mbox{angle from the horizontal.} \nonumber \end{eqnarray}$$

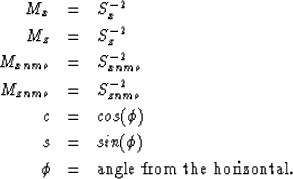This expression is called the double elliptic approximation. Dellinger and Muir (1991) demonstrate that this approximation accurately fits general transversely isotropic media.

In the cross-well geometry examples that follow, the estimated vertical slowness will be referred to as S_z rather than S_znmo.