As mentioned above, expression (5) will be used to
estimate the 2N-dimensional slowness vector ![]() given the traveltimes from a cross-well experiment. However,
we can investigate some of the difficulties in estimating such a vector
by first studying the case of a homogeneous medium (N=1)
given the traveltimes from a cross-well experiment. However,
we can investigate some of the difficulties in estimating such a vector
by first studying the case of a homogeneous medium (N=1)
When the model is isotropic, we usually estimate the slowness S of the homogeneous medium that best fits the traveltimes by simply averaging all the slownesses Si obtained from the individual rays:
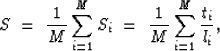 |
(7) |
When the model is anisotropic, the 2-D vector
![]() that best fit the traveltimes can be obtained
by generalizing
the average (7).
This
generalization is, as expected, in a least-squares sense. Note that
expression (1b) is linear in Sx2 and Sz2. Therefore, for a
given set of traveltimes and source-receiver
locations, it is possible to set up a least-squares problem to find
the vector
that best fit the traveltimes can be obtained
by generalizing
the average (7).
This
generalization is, as expected, in a least-squares sense. Note that
expression (1b) is linear in Sx2 and Sz2. Therefore, for a
given set of traveltimes and source-receiver
locations, it is possible to set up a least-squares problem to find
the vector ![]() of the
homogeneous medium. Defining
of the
homogeneous medium. Defining ![]() and
and ![]() ,the least-squares problem is
,the least-squares problem is
| (8) |
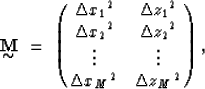
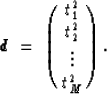
Equation (8) can be solved in different ways. The most popular approach is by using the normal equations, resulting
| (9) |
For estimating
Wx and Wz simultaneously and accurately,
![]() has to be well conditioned. Note that this is not the case
when most of the elements of the matrix satisfy
either
has to be well conditioned. Note that this is not the case
when most of the elements of the matrix satisfy
either ![]() or
or ![]() . These two
conditions describe cases when rays
are traveling close to the horizontal or the vertical. In such cases, it is
impossible to determine simultaneously
both components of the vector
. These two
conditions describe cases when rays
are traveling close to the horizontal or the vertical. In such cases, it is
impossible to determine simultaneously
both components of the vector ![]() because of
the limited view of the measurements translates
immediately into severe ill-conditioning.
This can be understood by trying to
estimate Wx and Wz from the simple cross-well experiment
shown in Figure
because of
the limited view of the measurements translates
immediately into severe ill-conditioning.
This can be understood by trying to
estimate Wx and Wz from the simple cross-well experiment
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , where
, where ![]() .In this case
.In this case
![]()
![]()
 |
In other words, the smallest eigenvalue (zero in this case) is
related to the vertical component of the slowness whereas the largest
one is related to the horizontal component.
On the contrary, for a VSP-like geometry largest eigenvalue
is related to Sz and the smallest one is related
to Sx (Dellinger, 1989).
Having more rays (M) without increasing the aperture
does not solve the problem. In such a case, the largest
eigenvalue of the matrix ![]() tends to
tends to
![]() and the smallest one tends to zero again.
and the smallest one tends to zero again.
The previous inversion scheme for homogeneous models
can be generalized for estimating ![]() in an heterogeneous medium. All we have to do is to solve systems of
equations like (8) at each cell.
In other words, the
problem in the heterogeneous model is separated into many subproblems
in homogeneous models.
This approach might be easily implemented when the ray paths
are used as basis functions for describing the slowness
(Harris et al., 1990a) if, instead of
averaging the slownesses of the different rays where they
intersect, system of equations like (8) are solved to estimate
the two components of the slowness.
in an heterogeneous medium. All we have to do is to solve systems of
equations like (8) at each cell.
In other words, the
problem in the heterogeneous model is separated into many subproblems
in homogeneous models.
This approach might be easily implemented when the ray paths
are used as basis functions for describing the slowness
(Harris et al., 1990a) if, instead of
averaging the slownesses of the different rays where they
intersect, system of equations like (8) are solved to estimate
the two components of the slowness.
Although this idea will not be
exploited
in the present paper, it can help us to understand
intuitively which components
of the slowness vector ![]() are easier (or more difficult)
to estimate from cross-well traveltimes measurements. In general, vertical
variations in the medium
are easier to estimate than horizontal variations.
Vertical variations correspond to singular vectors associated with
the largest singular values of the problem whereas lateral variations
are associated to the smallest singular values (Pratt and Chapman, 1990).
As explained earlier, in homogeneous models Sx
is related to the larger singular value and Sz is related to the
smaller one. Therefore, if the problem in a heterogeneous model
is solved as many separate subproblems in homogeneous models, the
largest singular values will be related to vertical
variations in Sx and the smallest ones will be related
to lateral variations in Sz. We will demonstrate in the field data
examples that estimating horizontal variations in Sz is indeed
a difficult problem whereas it is always easier to estimate
vertical variations in Sx.
are easier (or more difficult)
to estimate from cross-well traveltimes measurements. In general, vertical
variations in the medium
are easier to estimate than horizontal variations.
Vertical variations correspond to singular vectors associated with
the largest singular values of the problem whereas lateral variations
are associated to the smallest singular values (Pratt and Chapman, 1990).
As explained earlier, in homogeneous models Sx
is related to the larger singular value and Sz is related to the
smaller one. Therefore, if the problem in a heterogeneous model
is solved as many separate subproblems in homogeneous models, the
largest singular values will be related to vertical
variations in Sx and the smallest ones will be related
to lateral variations in Sz. We will demonstrate in the field data
examples that estimating horizontal variations in Sz is indeed
a difficult problem whereas it is always easier to estimate
vertical variations in Sx.
Equation (5) can be used
to estimate ![]() for all the cells
at the same time (rather than in a cell-by-cell basis,
as explained before).
This equation is obviously non-linear in Sj and
Sj+N. One way to solve the problem is by a sequence of
linearized steps. We start by approximating (5) by a first order
Taylor series expansion centered in a given model
for all the cells
at the same time (rather than in a cell-by-cell basis,
as explained before).
This equation is obviously non-linear in Sj and
Sj+N. One way to solve the problem is by a sequence of
linearized steps. We start by approximating (5) by a first order
Taylor series expansion centered in a given model ![]() :
:
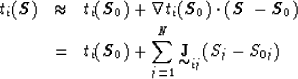 |
||
| (10) |
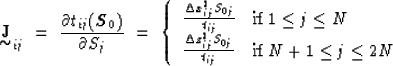
| (11) |
Note that the matrix ![]() depends explicitly on the slowness of the
reference model
depends explicitly on the slowness of the
reference model ![]() in contrast with the isotropic case
where the matrix depends only on the lengths of the rays in each pixel.
In the isotropic case if the rays are straight, the estimation
of the slowness becomes a linear problem because
in contrast with the isotropic case
where the matrix depends only on the lengths of the rays in each pixel.
In the isotropic case if the rays are straight, the estimation
of the slowness becomes a linear problem because ![]() is a constant.
In the anisotropic case, however, the problem is still non-linear even if the
rays are straight. Ray bending introduces another source of
non-linearity.
is a constant.
In the anisotropic case, however, the problem is still non-linear even if the
rays are straight. Ray bending introduces another source of
non-linearity.
In the examples shown later, equation
(11) will be solved using the LSQR variant of the conjugate
gradients algorithm (Nolet, 1987). We will show that
by doing a few iterations with this
method at each linearized step, the ill-conditioning
of ![]() caused by to the limited view of the measurements is
better handled
than by solving
the normal equations (in the overdetermined case).
caused by to the limited view of the measurements is
better handled
than by solving
the normal equations (in the overdetermined case).