




Next: Initial and boundary condition
Up: LINE SOURCE
Previous: LINE SOURCE
Let us suppose (x,z) are the coordinates before the rotation and
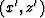 after the rotation. One can find the relations between
these two coordinates:
after the rotation. One can find the relations between
these two coordinates:
| 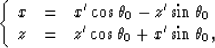 |
(7) |
where 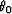 is the incident angle of the plane waves.
It is easy to show that both the eikonal equation and the orthogonal equation
are invariant under the transformation defined in equation (7).
Therefore, we can use equations (1) and (2)
after replacing (x,z) by
is the incident angle of the plane waves.
It is easy to show that both the eikonal equation and the orthogonal equation
are invariant under the transformation defined in equation (7).
Therefore, we can use equations (1) and (2)
after replacing (x,z) by 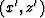 . The new definition of the
function p is as follows:
. The new definition of the
function p is as follows:
| 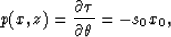 |
(8) |
where s0 is the slowness at the surface, and x0 is the surface location
of a incident ray. I do not know the meaning of p defined here.
I guess it is a horizontal traveltime.
Along each ray, p maintains to be constant.
Therefore, we can trace a ray by following the trajectory
of a contour line of p.





Next: Initial and boundary condition
Up: LINE SOURCE
Previous: LINE SOURCE
Stanford Exploration Project
12/18/1997
![]() after the rotation. One can find the relations between
these two coordinates:
after the rotation. One can find the relations between
these two coordinates: