Residual depth migration is the transformation from image
![]() to image Q(x,z).
The kinematic operator that effects this
transformation is defined by the mapping functions between the image locations
(x,z) and
to image Q(x,z).
The kinematic operator that effects this
transformation is defined by the mapping functions between the image locations
(x,z) and ![]() . In my last report, I showed that these mapping
functions are expressed implicitly in the following pair of equations:
. In my last report, I showed that these mapping
functions are expressed implicitly in the following pair of equations:
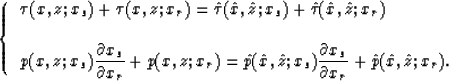 |
(1) |
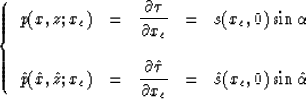 |
(2) |
The partial derivative of xs with respect to xr depends on the type of a data gather. For post-stack data,
![]()
![]()
![]()
For each image location (x,z) on Q(x,z), equation (1)
implicitly tells us the corresponding image location ![]() on
on ![]() . We want to solve
. We want to solve ![]() in this
equation as functions of (x,z). For general slowness models, this nonlinear
equation set has to be solved using a numerical method.
Searching is a straightforward method, in which, for each xr
and (x,z), all points around (x,z) are checked
to find the
in this
equation as functions of (x,z). For general slowness models, this nonlinear
equation set has to be solved using a numerical method.
Searching is a straightforward method, in which, for each xr
and (x,z), all points around (x,z) are checked
to find the ![]() that satisfies equation (1).
However, this algorithm is time-consuming, especially when the image dimensions
are large.
that satisfies equation (1).
However, this algorithm is time-consuming, especially when the image dimensions
are large.
I have developed an algorithm that solves equation (1) using finite-difference techniques. The ideas are similar to those used in the finite-difference calculation of traveltimes (Van Trier, 1990). The solution of equation (1) is known on the surface. We can extrapolate this solution in depth once we know the derivative of the solution with respect to the depth.