TWO WAY PHASE SHIFT MODELING

Two way phase shift modeling is a step-by-step approach to calculating the recorded particle velocities. The input to the process is a layered medium and a traction applied at the surface. The sequence of steps in the modeling algorithm is shown in figures  to .

 

pict1
Figure 1 The first step is to calculate the (complex) amplitudes of the three downgoing waves and the particle velocities generated by the traction. Each phase shift uses the vertical slowness appropriate for the wavetype.

 

pict2
Figure 2 The second step propagates the waves to the bottom of the layer. Each component of the downgoing wavefield is phase shifted using the Appropriate vertical slowness.

 

pict3
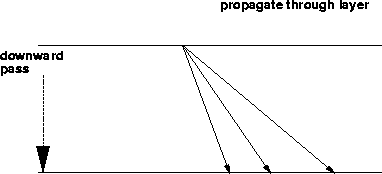
Figure 3 The third step calculates the transmitted downgoing wave amplitudes and the reflected upgoing wave amplitudes. The upgoing amplitudes are saved to be used later. Steps 2 and 3 are repeated until the bottom of the model is reached.

 

pict4
Figure 4 The fourth step propagates the upgoing waves in the last layer to the top of that layer.

 

pict5
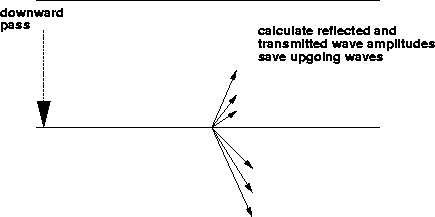
Figure 5 The fifth step calculates downgoing reflected wave amplitudes and upgoing transmitted wave amplitudes at the top of a layer. The upgoing reflected amplitudes at this interface that were saved is step 3 are added into the upgoing wavefield. The downgoing reflected amplitudes are saved to be used later. Steps 4 and 5 are repeated until the wavefield reaches the surface.

 

pict6
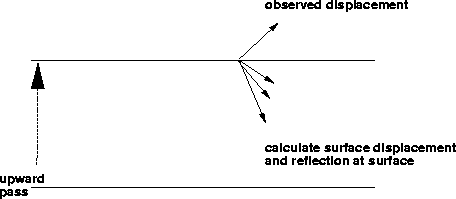
Figure 6 At the surface the reflected downgoing wavefield and the particle velocities at the free surface are calculated. The velocities are summed into the output particle velocity field. If multiples are to be modeled the downgoing wave field is used as the input to step 2. As the wavefield is propagated downwards the saved downgoing reflected amplitudes saved at each interface are added into the wavefield. Each pass down and up through the stack of layers adds one more set of multiples to the output displacement field.

The main loop of the program runs over the two horizontal slownesses p_x and p_y. For each (p_x,p_y) pair I calculate the amplitude of the recorded particle velocities at each frequency. The operators related to free surface and boundary effects are frequency independent as is the vertical slowness p_z. The only place that the frequency enters into the calculation is in the phase shift through each layer. The vertical wavenumber is given by 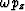$\omega p_z$. The frequency independence makes the process relatively cheap. The most expensive step is the calculation of the vertical slownesses and operators for each layer. This calculation is only performed once for all frequencies and for all orders of multiples. The application of the operators and the phase shifts is fully vectorized over frequency. I will now discuss each stage of the calculation. Most of the mathematical detail is in the appendix.