Next: CALCULATION OF THE TIME/SPACE
Up: TWO WAY PHASE SHIFT
Previous: Conversions at the surface
All the results that I will show in this paper are for a simple two layer
model. The bottom half space is isotropic and of very low density so that
there is a very high reflectivity for most angles. The surface layer is
highly anisotropic. It has orthorhombic symmetry with a horizontal plane
of symmetry. The medium is expected to exhibit triplication in the propagation
of shear waves. Most of the examples are for the response to a horizontal
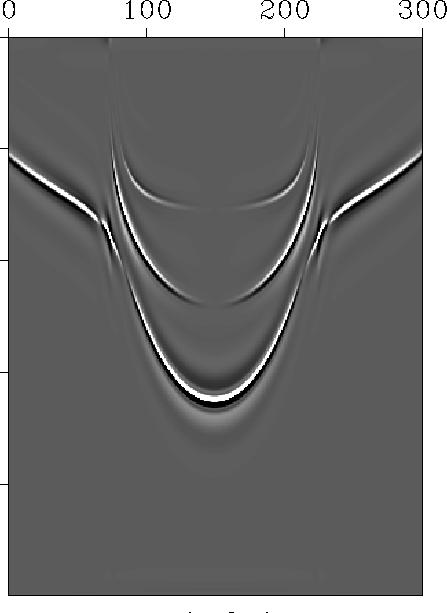
traction applied along the vertical symmetry plane. In figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I show the
I show the 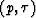 domain response for a run with no multiples and no
direct arrivals. The
domain response for a run with no multiples and no
direct arrivals. The 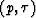 domain response is found by taking the
inverse fourier transform of the
domain response is found by taking the
inverse fourier transform of the 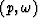 domain data that I have
calculated. The plot shows the x-component of displacement.
The uppermost event is the P-P wave reflection. The second
event is the P-S and S-P reflections. The third event which exhibits a
downwards concavity in the wavefront is the S-S wave reflection. The
range of p values used did not extend far enough to observe all of the
propagating S-waves.
Figure
domain data that I have
calculated. The plot shows the x-component of displacement.
The uppermost event is the P-P wave reflection. The second
event is the P-S and S-P reflections. The third event which exhibits a
downwards concavity in the wavefront is the S-S wave reflection. The
range of p values used did not extend far enough to observe all of the
propagating S-waves.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the same model but in this case the direct arrivals have
been calculated. Figure
shows the same model but in this case the direct arrivals have
been calculated. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the same model with the first order
multiples calculated. The P-P-P multiple is almost hidden behind the S-S
arrival. The final event is the S-S-S-S arrival, in between there are
multiples with mixed wavetypes, P-P-P-S, P-P-S-S, and P-P-P-S. This figure
is already somewhat confusing. One advantage of the phase shift method is that
I can easily ``turn off'' some of these events to obtain a clearer picture.
shows the same model with the first order
multiples calculated. The P-P-P multiple is almost hidden behind the S-S
arrival. The final event is the S-S-S-S arrival, in between there are
multiples with mixed wavetypes, P-P-P-S, P-P-S-S, and P-P-P-S. This figure
is already somewhat confusing. One advantage of the phase shift method is that
I can easily ``turn off'' some of these events to obtain a clearer picture.
pt1
Figure 7 Primaries only data in the 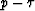 domain. Traction applied along x-axis, velocities measured along x-axis.
domain. Traction applied along x-axis, velocities measured along x-axis.
 pt2
pt2
Figure 8 Primaries + direct arrivals in the 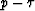 domain. Traction applied along x-axis, velocities measured along x-axis.
domain. Traction applied along x-axis, velocities measured along x-axis.
 pt3
pt3
Figure 9 Primaries and first order multiples in the 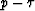 domain. Traction applied along x-axis, velocities measured along x-axis.
domain. Traction applied along x-axis, velocities measured along x-axis.






Next: CALCULATION OF THE TIME/SPACE
Up: TWO WAY PHASE SHIFT
Previous: Conversions at the surface
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I show the
I show the ![]() domain response for a run with no multiples and no
direct arrivals. The
domain response for a run with no multiples and no
direct arrivals. The ![]() domain response is found by taking the
inverse fourier transform of the
domain response is found by taking the
inverse fourier transform of the ![]() domain data that I have
calculated. The plot shows the x-component of displacement.
The uppermost event is the P-P wave reflection. The second
event is the P-S and S-P reflections. The third event which exhibits a
downwards concavity in the wavefront is the S-S wave reflection. The
range of p values used did not extend far enough to observe all of the
propagating S-waves.
Figure
domain data that I have
calculated. The plot shows the x-component of displacement.
The uppermost event is the P-P wave reflection. The second
event is the P-S and S-P reflections. The third event which exhibits a
downwards concavity in the wavefront is the S-S wave reflection. The
range of p values used did not extend far enough to observe all of the
propagating S-waves.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the same model but in this case the direct arrivals have
been calculated. Figure
shows the same model but in this case the direct arrivals have
been calculated. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the same model with the first order
multiples calculated. The P-P-P multiple is almost hidden behind the S-S
arrival. The final event is the S-S-S-S arrival, in between there are
multiples with mixed wavetypes, P-P-P-S, P-P-S-S, and P-P-P-S. This figure
is already somewhat confusing. One advantage of the phase shift method is that
I can easily ``turn off'' some of these events to obtain a clearer picture.
shows the same model with the first order
multiples calculated. The P-P-P multiple is almost hidden behind the S-S
arrival. The final event is the S-S-S-S arrival, in between there are
multiples with mixed wavetypes, P-P-P-S, P-P-S-S, and P-P-P-S. This figure
is already somewhat confusing. One advantage of the phase shift method is that
I can easily ``turn off'' some of these events to obtain a clearer picture.