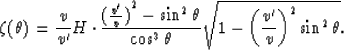Next: 8: CLASSIFICATION OF K-OPERATORS
Up: 7: GEOMETRICAL PROBLEMS OF
Previous: C. 15-degree algorithm in
We suggest that a reflector is flat: z=H.
First step: We represent travel-time dependence for common source gathered
in a true model in the following form:
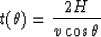
| 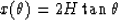 |
(76) |
where 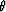 is incident angle.
is incident angle.
Second step: Reverse Eiconal's continuation can be determined with help of
ray's equations
| 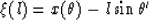 |
(77) |
| 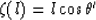 |
(78) |
where 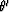 is incident angle of a ray which is correspondent to reverse
Eiconal's continuation:
is incident angle of a ray which is correspondent to reverse
Eiconal's continuation:
| 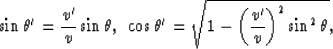 |
(79) |
l is a length of the ray from the point 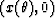 to the point
to the point
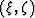 . So
. So
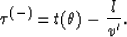
Third step: The location of the reflector's image can be found from
the condition 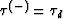 , that is
, that is
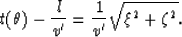
Having usage of equations (76), (77), (78), and (79),
we derive
![\begin{displaymath}
l={v^\prime \over v}{H \over \cos^{3} \theta } \cdot
\left[...
...t( {v^{\prime} \over v}\right) }^{2} \sin ^{2} \theta
\right].\end{displaymath}](img452.gif)
Now we substitute this formula into equations (77) and (78)
and finally get parametric descriptions of the reflector image:
![\begin{displaymath}
\xi (\theta )=2H\tan \theta \left[ 1-{{({v^{\prime} \over v})}^{2} - \sin^{2} \theta
\over 2\cos^{2} \theta} \right]\end{displaymath}](img453.gif)
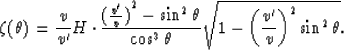





Next: 8: CLASSIFICATION OF K-OPERATORS
Up: 7: GEOMETRICAL PROBLEMS OF
Previous: C. 15-degree algorithm in
Stanford Exploration Project
1/13/1998
![]()
![]()
![]() , that is
, that is
![]()
![]()
![\begin{displaymath}
\xi (\theta )=2H\tan \theta \left[ 1-{{({v^{\prime} \over v})}^{2} - \sin^{2} \theta
\over 2\cos^{2} \theta} \right]\end{displaymath}](img453.gif)