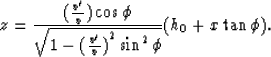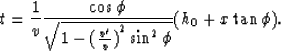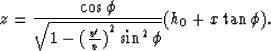Next: B. Two-layer media
Up: 7: GEOMETRICAL PROBLEMS OF
Previous: Geometrical analysis of imaging
Let equation
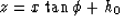
describe the location of a reflector.
First step: calculation of two-way zero-offset travel time in a true model:
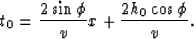
Second step: reverse Eiconal's continuation of t0(x) with wrong
velocity 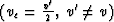 :
:
| 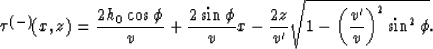 |
(73) |
Third step: imaging from the condition
| 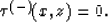 |
(74) |
Inserting equation (73) into equation (74) and solving with
respect to z, we derive location of the image in depth-section:
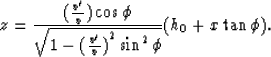
The reflection image in time section we receive after substitution 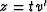 is:
is:
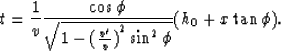
Time-to-depth migration in this situation is depth scaling with true velocity
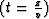 :
:
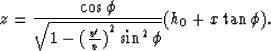
We see that depth scaling does not supply correct imaging, although the error is not big: it is proportional to 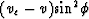 .
.





Next: B. Two-layer media
Up: 7: GEOMETRICAL PROBLEMS OF
Previous: Geometrical analysis of imaging
Stanford Exploration Project
1/13/1998
![]()
![]()
![]() :
: