




Next: Eikonal equation
Up: 3: WHY DISCONTINUITIES?
Previous: Characteristics
Let us assume that the solution 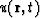 of the equation (18) has a ``weak discontinuity'', (i.e., discontinuity
of the order 2) on the surface
of the equation (18) has a ``weak discontinuity'', (i.e., discontinuity
of the order 2) on the surface 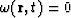 . This means that
. This means that
-
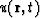 and all first derivatives are continuous when crossing the
surface
and all first derivatives are continuous when crossing the
surface 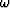 .
. -
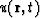 satisfies the equation (18) on each side of the surface
satisfies the equation (18) on each side of the surface
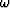 .
. - Some second derivatives have a jump when crossing the surface
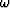 (they have two different values on both sides of the surface
(they have two different values on both sides of the surface 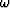 ).
).
But the latter is only possible when 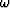 is a characteristic!
Otherwise, unique values of u and
is a characteristic!
Otherwise, unique values of u and 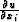 would
determine the unique values of all second derivatives on the surface
would
determine the unique values of all second derivatives on the surface 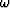 .
.
So a characteristic surface is the only possible location for a weak discontinuity
if it is a solution of the equation (18).
If this is valid for a weak discontinuity, it is also valid for
discontinuities of all orders if they represent jumps of derivatives with
respect to t. It follows through a simple consideration that: 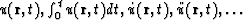 satisfy the same
equation (18), and we can always transform an arbitrary discontinuity
into a weak one.
satisfy the same
equation (18), and we can always transform an arbitrary discontinuity
into a weak one.





Next: Eikonal equation
Up: 3: WHY DISCONTINUITIES?
Previous: Characteristics
Stanford Exploration Project
1/13/1998
![]() of the equation (18) has a ``weak discontinuity'', (i.e., discontinuity
of the order 2) on the surface
of the equation (18) has a ``weak discontinuity'', (i.e., discontinuity
of the order 2) on the surface ![]() . This means that
. This means that
![]() satisfy the same
equation (18), and we can always transform an arbitrary discontinuity
into a weak one.
satisfy the same
equation (18), and we can always transform an arbitrary discontinuity
into a weak one.