Eikonal equation

The characteristic equation $\omega ({\bf r},t)=0$ describes the propagation of a discontinuity in space (x,y,z). Let us assume that equation $\omega =0$ can be solved with respect to t: $t=\tau({\bf r})$and $\omega \equiv t- \tau({\bf r})=0$. Then we get from equation (20):  

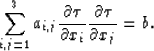$$\sum^{3}_{i,j=1} a_{i,j}{\partial\tau\over \partial x_{i}} {\partial\tau\over \partial x_{j}}=b.$$ (21)

That is exactly the Eikonal equation for a medium with elliptic anisotropy. In the case of isotropy, it follows that $a_{ik}=a\delta _{ik}$ and equation (21) is reduced to  

$${\left( {\partial\tau \over \partial x_{1}}\right) }^{2}+{\l... ...artial \tau \over \partial x_{3}}\right) }^{2}= {1 \over v^{2}}$$ (22)

$v=(\sqrt{{a\over b}})$.

Let us consider, for example, the linear acoustic equation

$${\rm div} (k {\rm grad}(u))=\rho {\partial^{2}u \over \partial t^{2}}$$

or

$$\sum^{3}_{i=1} {\partial \over \partial x_{i}} (k {\partial ... ...er \partial x_{i}})= \rho {\partial^{2}u \over \partial t^{2}}.$$

In this case $a_{ij}= k \delta _{ij}, b= \rho$ and we again get equation (22) at $v= (\sqrt{{k\over \rho}})$.It is very important that the propagation of a discontinuity depends only on senior terms of the equation (18).