




Next: About this document ...
Up: Popovici : PSPM analysis
Previous: References
The solutions to the partial differential equations (7) and
(8) are obtained using the method of characteristics.
The characteristic curves are curves on which the partial
differential equation in several independent parameters (in
our case the parameters (x0, t0) ) can be transformed
into a system of ordinary differential equations in a single
parameter along the characteristic curve.
A partial differential equation of the form

can be reduced to the form

if we can find a parameter  such that
such that

so that we can express the variables (x, t) in the form

As a result we have

which we can introduce in the original equation.
For equation (7) the system of associated equations is
|  |
(9) |
which after integration becomes
| ![\begin{displaymath}
\left \{ \begin{array}
{l}
\displaystyle{{{h^2-x^2} \over {x...
...\int{f_1[x(\tau),t(\tau)]\:d\tau} + c_3}}\\ \end{array} \right.\end{displaymath}](img27.gif) |
(10) |
The constants c1, c2, c3 are functions of the parameter
given on the initial curve, and are determined by setting  in equations (10).
in equations (10).
The initial condition is given along an ellipse, and has the form
|  |
(11) |
As a result the solution for the function u is given
in parametric form
|  |
(12) |
For equation 8 the system of associated equations is
|  |
(13) |
which after integration becomes
| ![\begin{displaymath}
\left \{ \begin{array}
{l}
\displaystyle{{\sqrt{h^2-x^2}} c_...
...\int{f_2[x(\tau),t(\tau)]\:d\tau} + c_3}}\\ \end{array} \right.\end{displaymath}](img32.gif) |
(14) |
The constants c1, c2, c3 are functions of the parameter
given on the initial curve, and are determined by setting  in equations (14).
in equations (14).
The initial condition is given along a curve of constant 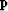 parameter, and has the form
parameter, and has the form
|  |
(15) |
As a result the solution for the function u is given
in parametric form
|  |
(16) |
The amplitudes of the function u along the characteristic curves
are found by calculating the integrals in
equations (9) and (14).





Next: About this document ...
Up: Popovici : PSPM analysis
Previous: References
Stanford Exploration Project
1/13/1998
![]()
![]()

![]()
![]()

![\begin{displaymath}
\left \{ \begin{array}
{l}
\displaystyle{{{h^2-x^2} \over {x...
...\int{f_1[x(\tau),t(\tau)]\:d\tau} + c_3}}\\ \end{array} \right.\end{displaymath}](img27.gif)



![\begin{displaymath}
\left \{ \begin{array}
{l}
\displaystyle{{\sqrt{h^2-x^2}} c_...
...\int{f_2[x(\tau),t(\tau)]\:d\tau} + c_3}}\\ \end{array} \right.\end{displaymath}](img32.gif)
![]() parameter, and has the form
parameter, and has the form

