




Next: NON-HYPERBOLIC MOVEOUT EQUATIONS
Up: ANELLIPTIC APPROXIMATION
Previous: Byun's approximation
From this viewpoint, the deviation term of Muir's approximation can be put into the form
| 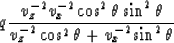 |
(4) |
This equation also has zero value in the vertical and horizontal directions and maximum value near 45 degrees because it contains the 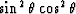 , but has a kind of weighting along the angle that causes a little movement of the maximum value according to the anisotropy factor, defined as the horizontal to vertical phase velocity ratio
, but has a kind of weighting along the angle that causes a little movement of the maximum value according to the anisotropy factor, defined as the horizontal to vertical phase velocity ratio 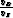 . In this case the ray velocity can be represented by
. In this case the ray velocity can be represented by
| 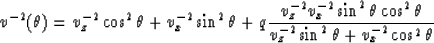 |
(5) |
Figure 2 and Figure 3 show how well these two approximations for deviation term fit to the deviation from the best fitting ellipse in the cases of weak and moderate anisotropy, respectively.





Next: NON-HYPERBOLIC MOVEOUT EQUATIONS
Up: ANELLIPTIC APPROXIMATION
Previous: Byun's approximation
Stanford Exploration Project
1/13/1998