ANELLIPTIC APPROXIMATION

Among the many types of deviation from isotropy, the most probable form for normal earth sections is called transverse isotropy. Transverse isotropy assumes that physical properties are the same in all planes perpendicular to one axis of symmetry. In transverse isotropy, the group velocity curve, which is a graph of the velocity of energy propagation versus the angle of energy propagation, does not define an ellipse for ¶-wave or qSV-wave, but the velocity for qSH-wave is elliptical. So the elliptical approximation as velocity equation of transverse isotropy which results in the hyperbolic moveout equation is usually inappropriate and misleading for ¶- and qSV-waves. Good approximations might include the additional term which represents the deviation from the best fitting ellipse.

Assuming the velocity deviation from the ellipse has typical pattern, the approximation for the ray velocity of transverse isotropy can be represented by the form

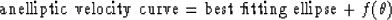$$\hbox{\rm anelliptic velocity curve}=\hbox{\rm best fitting ellipse} + f(\theta)$$ (1)

where the best fitting ellipse means the ellipse that has the same vertical and horizontal velocity as the anisotropic velocity curve and where 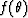$f(\theta)$ corresponds to the deviation from the best fitting ellipse.

Figure 1 shows ray velocity deviations from the best fitting ellipse in several transversely isotropic models in terms of sloth (inverse velocity squared) and shows patterns that have zero value in the vertical and horizontal directions and a maximum value of about 45 degrees.