




Next: EXAMPLES
Up: FINITE-DIFFERENCE SCHEME
Previous: FINITE-DIFFERENCE SCHEME
We have presented the numerical scheme in polar coordinates for the
sole purpose of solving the point-source problem. In polar coordinates
the initial condition at the source is easily specified as 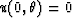 .
However, the same problem may be solved in Cartesian coordinates if calculations
are done on a sequence of expanding rectangular fronts. Although
slightly more
complicated, this approach saves the cost of mapping the slowness
and traveltime fields to and from polar coordinates. The rectangular
computational fronts are also used by Vidale (1988).
.
However, the same problem may be solved in Cartesian coordinates if calculations
are done on a sequence of expanding rectangular fronts. Although
slightly more
complicated, this approach saves the cost of mapping the slowness
and traveltime fields to and from polar coordinates. The rectangular
computational fronts are also used by Vidale (1988).
When one assumes outgoing rays at the boundaries, one-sided finite-differences
can be used at the left and right sides of the model.
These boundary conditions are of the same order as the scheme
inside the model, and generally do not cause any problems.
After  has been computed, traveltimes are calculated by
integrating
has been computed, traveltimes are calculated by
integrating 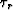 over
over  using a simple trapezoidal rule,
where
using a simple trapezoidal rule,
where 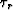 is found from equation (5).
is found from equation (5).





Next: EXAMPLES
Up: FINITE-DIFFERENCE SCHEME
Previous: FINITE-DIFFERENCE SCHEME
Stanford Exploration Project
1/13/1998
![]() has been computed, traveltimes are calculated by
integrating
has been computed, traveltimes are calculated by
integrating ![]() over
over ![]() using a simple trapezoidal rule,
where
using a simple trapezoidal rule,
where ![]() is found from equation (5).
is found from equation (5).