




Next: Throw out the model
Up: CLASH IN PHILOSOPHIES
Previous: Rate of convergence
Philosophically,
what is the role of the nonlinear step on the missing data estimation?
The conventional wisdom is that before you begin linear estimation
you somehow measure the covariance matrix of the noise.
The covariance matrix of the solution is taken to be a prior(!).
During linear estimation these covariance matrices are constants.
In real life,
by which I mean (1) practical deconvolution filter design,
(2) the missing data estimation I showed a few weeks ago in
my textbook, and (3) in this paper, and probably other places too,
the estimation of the covariance matrices proceeds simultaneously
with the optimization, and it too is an optimization problem.
The nonlinear step accomodates
the limitation of the maximum-liklihood estimation paradyme
that the residual covariance matrix be a prior.
The Burg procedure is linear only because it is a sequence of linear
estimations of reflection coefficients, each based on the previous.
The missing-data-unknown-filter program missif()
is intrinsically nonlinear
(given the prior constraint that a filter be of prediction error form
and given some of the data values are known,
find the filter and the missing data values
to minimize output power).
The sparse dip spectrum problem addressed in this paper
is essentially nonlinear,
which is why this paper gives so much emphasis on good starting estimates.
Note that we do not really find the inverse covariance matrix,
but an approximate factorization of it,
the prediction-error filter (prediction in space).
Both problems are characterized by a vanishing of the model  and the partial derivative matrix
and the partial derivative matrix 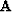 .There is nothing left here but the missing data
and the unknown filter (which is the factored covariance matrix).
So this activity doesn't fit academic inversion theory at all.
.There is nothing left here but the missing data
and the unknown filter (which is the factored covariance matrix).
So this activity doesn't fit academic inversion theory at all.





Next: Throw out the model
Up: CLASH IN PHILOSOPHIES
Previous: Rate of convergence
Stanford Exploration Project
1/13/1998