MODELING BY RESTORATION OF MISSING DATA

We take data space to be a uniform mesh on which some values are given and some are missing. We rarely have missing values on a time axis, but commonly have missing values on a space axis, i.e. missing seismograms. Missing seismograms (traces) happen occasionally for miscellaneous reasons and they happen systematically from aliasing and truncation. The aliasing arises from economic reasons--saving instrumentation by running receivers far apart. Truncation arises at the ends of any survey, which like any human activity, must be finite. Beyond the survey lies more hypothetical data. The traces we will find for the missing data are not as good as real observations, but they are closer to reality than supposing unmeasured data is zero-valued. Making an image with a single application of a conjugate operator amounts to assuming data vanishes beyond its given locations. Dealing with missing data is a step beyond this and, as we'll see, reduces the need for arbitrary model filtering.

The first principle we use for restoring missing data is that the restored data, after specified filtering, have minimum energy. Specifying the filter chooses the interpolation philosophy. Generally the filter is a roughening filter. When a roughening filter goes off the end of smooth data it typically produces a big edge transient. Minimizing energy implies a choice for unknown data values at the edge to minimize the transient. We'll examine five cases and then make some generalizations.

Let m denote a missing value. The data set on which the examples are based is $(\cdots, m, m, 1, m, 2, 1, 2, m, m, \cdots )$.Using a program described later, values were found to replace the missing m values so that the power in the filtered data is minimized. Figure 1 shows interpolation of the data set with 1-Z as a roughening filter. The interpolated data matches the given data where it is given.

 

mlines Figure 1 Top is given data. Middle is given data with interpolated values. Missing values seem to be interpolated by straight lines. Bottom shows the filter (1,-1).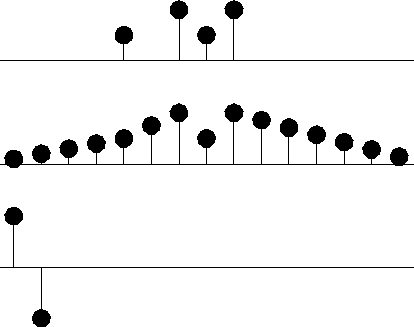

 

mparab Figure 2 Top is the same input data as in Figure 1. Middle is interpolated. Bottom shows the filter (-1,2,-1). Missing data seems to be interpolated by parabolas.

 

mseis Figure 3 Top is the same input. Middle is interpolated. Bottom shows the filter (1,-3,3,-1). Missing data is very smooth. It shoots upward high off the right edge of the observations apparently to match data slope there.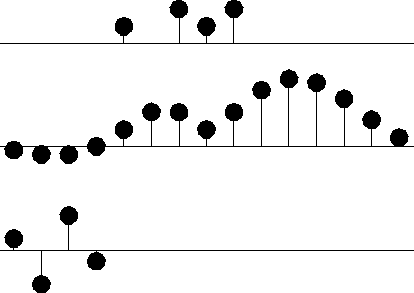

 

msmo Figure 4 Top is the same. Middle is interpolated. Bottom shows the filter (-1,-1,4,-1,-1). Interpolation is with stiff lines like the straight lines of Figure 1 but they project through a cluster of given values instead of projecting to the nearest given value. Thus this interpolation tolerates noise in the given data better than Figure 3.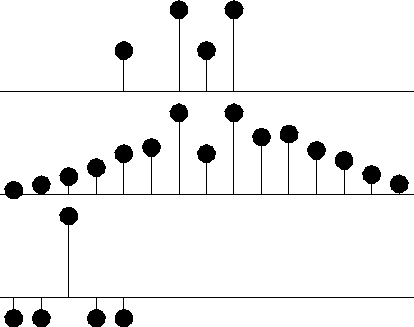

 

moscil Figure 5 Top is the same. Middle is interpolated. Bottom shows the filter (1,1). The interpolation is rough. Like the given data itself it has much energy at the Nyquist frequency. But unlike the given data it has little zero frequency energy.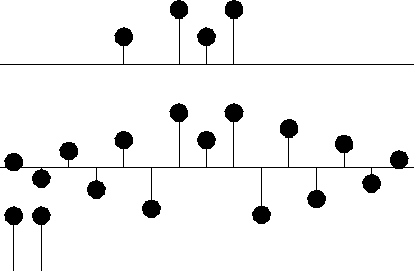

Figures 1-5 illustrate the rougher the filter the smoother the interpolated data, and vice versa. It is as if the product of the filter spectrum with the data spectrum is roughly constant. Switch attention from the residual spectrum to the residual itself. The residual for Figure 1 is the slope of the signal (because the filter 1-Z is a first derivative) and the slope is constant (uniformly distributed) along the straight lines where the least-squares procedure is choosing signal values. So these examples confirm the idea that the least-squares method abhors large values (because they are squared) and thus it tends to uniformly distribute residuals in both time and frequency to the extent the constraints allow. This idea helps us answer the question, ``What is the best filter to use?'' Formally the answer is that the filter should have an amplitude spectrum that is inverse to that we wish for the interpolated data. A systematic approach is developed in chapter 8 but I'll offer a simple subjective analysis here. Looking at the data I see all points are positive so it seems the data is rich in low frequencies so the filter should contain something like (1-Z) which vanishes at zero frequency. Likewise the data seems to contain Nyquist frequency so the filter should contain (1+Z). The result of the filter (1-Z)(1+Z)=1-Z<sup>2</sup> is in Figure 6. I regard this as the ``best'' interpolation based on the idea that the missing data should look like the given data.

 

mbest Figure 6 Top is the same. Middle is interpolated. Bottom shows the filter (1,0,-1) which comes from the coefficients of (1-Z)(1+Z). Both the given data and the interpolated data have significant energy at both zero and Nyquist frequencies.