Theory

The isotropic eikonal equation is  

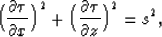$$\Bigl( { \partial \tau \over \partial x } \Bigr)^2 + \Bigl( { \partial \tau \over \partial z } \Bigr)^2 = s^2 ,$$ (1)

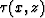where $\tau(x,z)$ gives the traveltime of some event at each point in space, and s(x,z) gives the slowness (inverse velocity) at each point in space. Van Trier and Symes (1990) start from this equation (equation (1) in their paper) and derive a traveltime extrapolation equation.

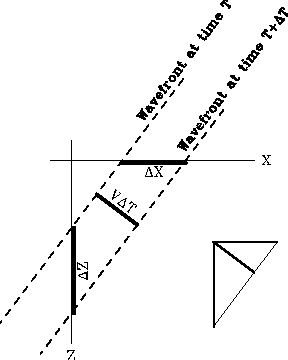
What does equation (1) represent? Figure 1 shows a tiny portion of a wavefront at two closely-spaced instants in time. On this scale, the wavefront can be approximated as a plane wave. The plane wave is moving along in some arbitrary direction with a velocity V, so it travels a distance $V \Delta T$ between the two times. At the same time, the plane wave also moves a distance $\Delta X$ along the X axis and $\Delta Z$ along the Z axis.

 

planar
Figure 1 Geometrical properties of plane-wave propagation.

The triangle to the lower right of Figure 1 has sides of length $\Delta X$ and $\Delta Z$ meeting at a right angle, and a height of $V \Delta T$ (if the hypotenuse is considered the base). Three applications of Pythagoras' theorem (one for each of the three right triangles involved) and a little algebra show that  

$$\Bigl( V \Delta T \Bigr)^2 = { \Delta X^2 \Delta Z^2 \over \Bigl( \Delta X^2 + \Delta Z^2 \Bigr) }$$ (2)

and thus  

$$\Bigl({ \Delta T \over \Delta X }\Bigr)^2 + \Bigl({ \Delta T \over \Delta Z }\Bigr)^2 = { 1 \over V^2 } = s^2 .$$ (3)

Hence, equation (1) does have a simple geometrical meaning.

How do we make equation (1) anisotropic? From the previous two paragraphs, we can see that ${ \partial \tau / \partial x }$in equation (1) (or $\Delta T / \Delta X$ in equation (3)) is just the horizontal phase slowness. For a monochromatic plane wave this is $k_x / \omega$.Similarly, ${ \partial \tau / \partial z } = k_z / \omega$.This lets us rewrite equation (1) as a dispersion relation:  

$$\Bigl( { k_x \over \omega } \Bigr)^2 + \Bigl( { k_z \over \omega } \Bigr)^2 = s^2 .$$ (4)

(This is just the Fourier-transformed homogeneous wave equation. Fourier-transformation breaks the wavefield up into plane-wave components.)

Recast as a dispersion relation, F(u) in equation (4) of Van Trier and Symes has a simple interpretation: u is a horizontal phase slowness $k_x / \omega$, and F(u) is a vertical phase slowness $k_z / \omega$.Replacing the isotropic dispersion relation in their paper with an appropriate anisotropic one gives an anisotropic traveltime extrapolation equation. Unfortunately, solving for k_z as a function of k_x can be difficult for some anisotropic media. In the general case of arbitrary three-dimensional anisotropy it can require solving a sixth order polynomial.