




Next: Summary of the transforms
Up: EXPRESSIONS OF THE PARABOLIC
Previous: Inverse transformation
Up to now, I only spoke of the overdetermined problem, which implies
the inversion of the matrix LTL. Things are different in the
underdetermined case, where we have to invert LLT. Effectively, this
matrix is not Toeplitz, even for a regular sampling in offset. The expression
of a component of LLT is:
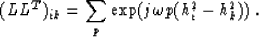
With a regular sampling 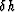 in offset, supposing h0=0,
this term becomes:
in offset, supposing h0=0,
this term becomes:
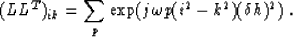
Consequently, (LLT)ik does not depend only on 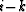 , and the
structure of the matrix LLT is not Toeplitz. So, it is not possible
to use Levinson algorithm in the underdetermined transformation
, and the
structure of the matrix LLT is not Toeplitz. So, it is not possible
to use Levinson algorithm in the underdetermined transformation
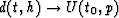 , where we have more parameters
p than offsets h.
, where we have more parameters
p than offsets h.
We can reason similarly for the transform
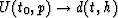 . Suppose that, rather than using simply the
modeling matrix L, we want to compute the least-squares inverse of LT:
(LLT)-1L in the overdetermined case, (LTL)-1LT in the
underdetermined case. Thus, Levinson algorithm could only be applied in
the underdetermined case.
. Suppose that, rather than using simply the
modeling matrix L, we want to compute the least-squares inverse of LT:
(LLT)-1L in the overdetermined case, (LTL)-1LT in the
underdetermined case. Thus, Levinson algorithm could only be applied in
the underdetermined case.





Next: Summary of the transforms
Up: EXPRESSIONS OF THE PARABOLIC
Previous: Inverse transformation
Stanford Exploration Project
1/13/1998
![]()
![]()
![]() . Suppose that, rather than using simply the
modeling matrix L, we want to compute the least-squares inverse of LT:
(LLT)-1L in the overdetermined case, (LTL)-1LT in the
underdetermined case. Thus, Levinson algorithm could only be applied in
the underdetermined case.
. Suppose that, rather than using simply the
modeling matrix L, we want to compute the least-squares inverse of LT:
(LLT)-1L in the overdetermined case, (LTL)-1LT in the
underdetermined case. Thus, Levinson algorithm could only be applied in
the underdetermined case.