




Next: Geometrical representation of
Up: SAMPLING IN VELOCITY DOMAIN
Previous: Examples of matrices
To compare the various ways of sampling in velocity domain,
we should choose some criterion.
A condition number of a matrix appears to be useless here,
as we can see from Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
All the matrices are singular.
Figure
.
All the matrices are singular.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c gives us a clue to the means of comparison.
Two curves are plotted in this figure. One represents singular values
of the matrix
c gives us a clue to the means of comparison.
Two curves are plotted in this figure. One represents singular values
of the matrix 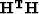 for ten velocities (the smoother one), and
the other, for two velocities. The matrix for two velocities is evidently
singular and the data cannot be restored when this matrix is used.
The curve of singular values of this matrix drops faster to the zero level.
The distribution of singular values for the matrix of ten velocities is
more uniform.
for ten velocities (the smoother one), and
the other, for two velocities. The matrix for two velocities is evidently
singular and the data cannot be restored when this matrix is used.
The curve of singular values of this matrix drops faster to the zero level.
The distribution of singular values for the matrix of ten velocities is
more uniform.
Let us analyze the curves in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a from this point of view.
There are four curves in the figure, which from the left to the right
(upper parts of the curves)
represent singular values of matrices computed for even sampling in
sloth, slowness, velocity and alacrity domains.
This is the succession according to the above criterion.
The velocity and alacrity curves have evidently worse behavior. The difference
between the sloth and slowness curves is much less.
The difference between the sloth and slowness curves in Figure
a from this point of view.
There are four curves in the figure, which from the left to the right
(upper parts of the curves)
represent singular values of matrices computed for even sampling in
sloth, slowness, velocity and alacrity domains.
This is the succession according to the above criterion.
The velocity and alacrity curves have evidently worse behavior. The difference
between the sloth and slowness curves is much less.
The difference between the sloth and slowness curves in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d
is almost nil. In this figure high velocities were not included. In the
region of high velocities slowness has worse behavior than sloth.
d
is almost nil. In this figure high velocities were not included. In the
region of high velocities slowness has worse behavior than sloth.
Singular values for matrices 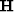 are in Figure
are in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
They should be the square roots of those in Figure
b.
They should be the square roots of those in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a.
This relationship holds for about the first 150 singular
values. It does not hold for the rest of the values because of the limited computational
precision (double precision used).
a.
This relationship holds for about the first 150 singular
values. It does not hold for the rest of the values because of the limited computational
precision (double precision used).





Next: Geometrical representation of
Up: SAMPLING IN VELOCITY DOMAIN
Previous: Examples of matrices
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a from this point of view.
There are four curves in the figure, which from the left to the right
(upper parts of the curves)
represent singular values of matrices computed for even sampling in
sloth, slowness, velocity and alacrity domains.
This is the succession according to the above criterion.
The velocity and alacrity curves have evidently worse behavior. The difference
between the sloth and slowness curves is much less.
The difference between the sloth and slowness curves in Figure
a from this point of view.
There are four curves in the figure, which from the left to the right
(upper parts of the curves)
represent singular values of matrices computed for even sampling in
sloth, slowness, velocity and alacrity domains.
This is the succession according to the above criterion.
The velocity and alacrity curves have evidently worse behavior. The difference
between the sloth and slowness curves is much less.
The difference between the sloth and slowness curves in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d
is almost nil. In this figure high velocities were not included. In the
region of high velocities slowness has worse behavior than sloth.
d
is almost nil. In this figure high velocities were not included. In the
region of high velocities slowness has worse behavior than sloth.