




Next: PARTIAL NORMAL MOVEOUT
Up: Jedlicka: Cascaded normal moveout
Previous: Introduction
Let us repeat basic definitions from Claerbout's paper.
A truncated Taylor series of the normal moveout equation is given by
the equation:
| 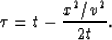 |
(1) |
The Nth partial normal moveout is given by the equation:
| 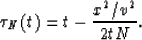 |
(2) |
The Nth partial normal moveout can be applied N times:
| 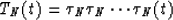 |
(3) |
The equation to be proved is
| 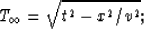 |
(4) |
i.e., normal moveout can be expressed as a superposition
of N Nth partial normal moveouts with arbitrary precision as
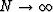 .
.





Next: PARTIAL NORMAL MOVEOUT
Up: Jedlicka: Cascaded normal moveout
Previous: Introduction
Stanford Exploration Project
1/13/1998