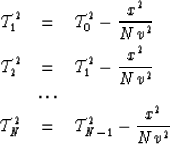Next: PROOF FOR 15-DEGREE PARTIAL
Up: Jedlicka: Cascaded normal moveout
Previous: 15-DEGREE PARTIAL NORMAL MOVEOUT
The case of the Nth partial normal moveout that is not a truncated
Taylor series is easier, so let us examine it first.
Define now the Nth partial normal moveout by
| 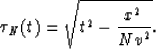 |
(5) |
We can see that the truncated Taylor series of equation (5)
is equation (2).
Now we will prove that
| 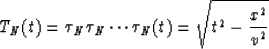 |
(6) |
holds exactly for all N.
Let us denote the application of the Nth partial normal moveout i times by
| 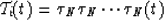 |
(7) |
It holds true that
| 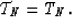 |
(8) |
The superposition of Nth partial normal moveouts may be written
| 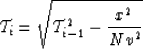 |
(9) |
for 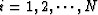 and
and 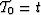 .Let us rewrite this equation into a system of equations:
.Let us rewrite this equation into a system of equations:
| 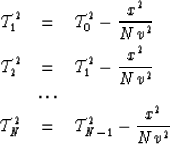 |
(10) |
| (11) |
| (12) |
| (13) |
By summing up all the equations we get
| 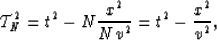 |
(14) |
which is the desired result.





Next: PROOF FOR 15-DEGREE PARTIAL
Up: Jedlicka: Cascaded normal moveout
Previous: 15-DEGREE PARTIAL NORMAL MOVEOUT
Stanford Exploration Project
1/13/1998