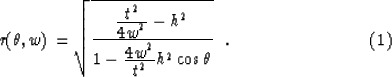
The impulse response of constant-velocity constant-offset migration is an ellipse with foci at source and receiver. Each point on the impulse response ellipse represents a different time dip in the data. A small segment of a dipping reflection event assumed to contain only a single traveltime dip, after migration becomes the tangent to the impulse response ellipse for the appropriate traveltime. The traveltime determines the size of the ellipse, and the traveltime dip determines the position of the image along the impulse response ellipse. Seen in reverse, given an image point and its depth dip, we can solve for the position of the source and receiver that have an impulse response that goes through our point and is tangent to the dipping reflector segment.
Starting at some point in depth with an assumed dip and solving for the source and receiver points that contain a specular reflection from the point, we can write an equation in polar coordinates that describes the migration ellipse that goes through the point.
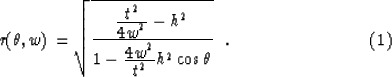
![]()
![\begin{displaymath}
{\partial t \over \partial y}=w \biggl[{r(\theta) \cos \thet...
...^2(\theta)+h^2+2r(\theta)h \cos \theta}}\biggr] \ \ .
\eqno (3)\end{displaymath}](img6.gif)
After choosing an initial depth and depth dip and solving for the shot receiver pair, equations (1)-(3) give the traveltime and traveltime dip of the specular reflection from that point. When the migration slowness changes, the migration ellipse will move to a new position. The key to finding the position of the reflector as the slowness changes is to remember that the traveltime, midpoint, and traveltime dip of the reflector segment in the constant-offset section is fixed. Only its image in depth changes as the migration slowness changes. First, find a new impulse response after the migration slowness changes for the original shot-receiver pair that has the same traveltime as the previous impulse response at the old migration velocity. Then find a point on the new impulse response that has the same traveltime dip as the original point using the original migration slowness. This procedure gives the new location and dip of the event. Keeping t fixed as the traveltime of a reflection from our original point, the equation of the new impulse response ellipse at slowness wn can be written as
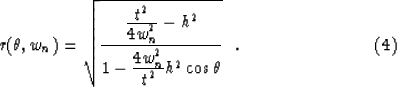
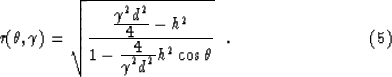
The time dip imaged at any point on the new impulse response ellipse is likewise given by:
![]()
Equating traveltime dip of the reflector at the
new and original slownesses and plugging in the
new relation for ![]() which equates the traveltimes
gives
a single equation to solve for
which equates the traveltimes
gives
a single equation to solve for
![]() as a function
of
as a function
of ![]() and the position of the original point.
and the position of the original point.
![\begin{displaymath}
\gamma \biggl[{r(\theta_0,d) \cos \theta_0 -h \over \sqrt
{r...
...ta_0, d)+h^2+2r(\theta_0, d)h \cos \theta_0}}
\biggr]
\eqno (7)\end{displaymath}](img15.gif)
![]()
Unfortunately, equation (7) is very difficult to solve analytically except for the trivial cases of zero dip or zero offset. To compute the operator I solve equation (7) numerically using Newton's method for finding roots.
Converting the solution of equation (7) back to Cartesian
coordinates gives ![]() and
and ![]() ,the new position of the dipping reflector segment as shown in
Figure 2.
,the new position of the dipping reflector segment as shown in
Figure 2.
Solving equation (7) for an initial depth and all initial dips
will trace out the ``spraying" operator for residual constant-offset
migration. The operator traces out the new
positions of events for a range of dips
after the migration slowness changes
for a fixed original point in the image.
This curve
is also the summation path if we change the role of
starting and final points by redefining ![]() .It is often more convenient to write the computer
code in terms of a summation operator. The
equations are symmetric so the summation operator for
.It is often more convenient to write the computer
code in terms of a summation operator. The
equations are symmetric so the summation operator for
![]() is the ``spraying" operator for
is the ``spraying" operator for ![]() .
.
Figure 3 shows an example of the summation operator when the slowness increases. Depending on the change in migration slowness and the initial depth of the reflector, the operator can triplicate.
This happens for image points
with large offset/depth ratio. Figure 4 shows an examples of
the residual migration operators for ![]() less than
one, when slowness decreases.
less than
one, when slowness decreases.
To get the correct amplitudes along the summation operator, compute the points on the summation operators in equal dip angle increments in the original image. To prevent operator aliasing I resample the summation operators in equal arclength along the summation trajectory. To recover equal dip weighting of the image, the amplitude along the summation path can be taken as the jacobian of the change of variables from arclength to dip angle.