




Next: Resolution of the normal
Up: Lp MINIMIZATION WITH THE
Previous: Normal equations
At the iteration k+1, the algorithm solves:
by taking:
- W0 = In (Identity matrix), at the first iteration,
- Wk formed with the residuals of iteration k (rk=y-Axk), at the
iteration k+1 .
Byrd and Payne (1979) showed that this algorithm is convergent under two
conditions:
- W(i) must be non-increasing in |r(i)|,
- W(i) must be bounded for all i.
The first condition is satisfied for 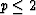 ; to assure the second
condition, Huber (1981) suggested replacing equation (3) with:
; to assure the second
condition, Huber (1981) suggested replacing equation (3) with:
|  |
(7) |
for a small positive constant  .
.
Equations (6) are the normal equations of the least-squares
minimization of:

Wk has the role of a weighting matrix, the inverse of a
covariance matrix. By giving the large residuals small weights
(or large variances), it reduces their role; on the contrary, well predicted
values will be given large weights (small variances). Aberrant values,
receiving low weights, will have a small influence: this makes the algorithm
robust, less sensitive to noise bursts in the data. This is especially true for
the extreme case p=1, as it had been predicted by Claerbout and Muir (1973).
However, the L1 norm is not strictly convex; so, the L1 minimization
problem might have non-unique solutions. The IRLS algorithm will lead
us to one of these solutions. The fact that the first iteration (W0=In)
is a least-squares inversion makes me think that this algorithm will lead us
to a solution close to the L2 solution. The choice of W0(i)=|y(i)|p-2
is not reasonable: during the
algorithm, x stays close to 0, and the algorithm converges (if it does) to
a vector  also close to zero, the residuals staying close to the
original vector y.
also close to zero, the residuals staying close to the
original vector y.





Next: Resolution of the normal
Up: Lp MINIMIZATION WITH THE
Previous: Normal equations
Stanford Exploration Project
1/13/1998
![]()
![]() also close to zero, the residuals staying close to the
original vector y.
also close to zero, the residuals staying close to the
original vector y.