 |
 |
 |
 | Preconditioning a non-linear problem and its application to bidirectional deconvolution |  |
![[pdf]](icons/pdf.png) |
Next: Application to Bidirectional Deconvolution
Up: Theory
Previous: Theory
We start from fitting goals
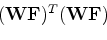 |
(1) |
and change variables from
 to
to
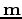 using
using
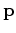 :
:
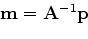 |
(2) |
Without preconditioning, we have the search direction
![$\displaystyle \Delta {\mathbf{m}}_{{\text{bad}}} = [\begin{array}{*{20}c} {{\ma...
...}{*{20}c} {{\mathbf{r}}_d } \\ {{\mathbf{r}}_m } \\ \par \end{array} } \right],$](img14.png) |
(3) |
and with preconditioning, we have the search direction
![$\displaystyle \Delta {\mathbf{p}}_{{\text{good}}} = [\begin{array}{*{20}c} {({\...
...}{*{20}c} {{\mathbf{r}}_d } \\ {{\mathbf{r}}_m } \\ \par \end{array} } \right].$](img15.png) |
(4) |
The essential feature of preconditioning is not that we perform the
iterative optimization in terms of the variable
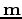 , but that we use a search direction that is a gradient
with respect to
, but that we use a search direction that is a gradient
with respect to
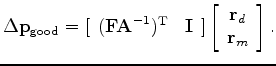 , not
, not
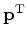 . Using
. Using
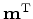 we have
we have
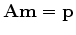 . This enables us to define a good
search direction in model space:
. This enables us to define a good
search direction in model space:
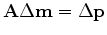 |
(5) |
We define the gradient by
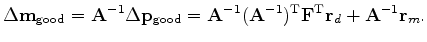 and notice that
and notice that
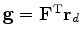 .
.
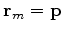 |
(6) |
The search direction (6) shows a positive-definite operator
scaling the gradient. All components of any gradient vector are
independent of each other and independently point to a direction for
descent. Obviously, each can be scaled by any positive number. Now we
have shown that we can also scale a gradient vector by a positive
definite matrix and still expect the conjugate-direction
algorithm to descend, as always, to the ``exact'' answer in a finite
number of steps. This is because modifying the search direction with
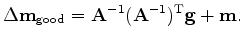 is equivalent to solving a
conjugate-gradient problem in
is equivalent to solving a
conjugate-gradient problem in
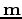 .
.
 |
 |
 |
 | Preconditioning a non-linear problem and its application to bidirectional deconvolution |  |
![[pdf]](icons/pdf.png) |
Next: Application to Bidirectional Deconvolution
Up: Theory
Previous: Theory
2011-09-13
 to
to
![$\displaystyle \Delta {\mathbf{m}}_{{\text{bad}}} = [\begin{array}{*{20}c} {{\ma...
...}{*{20}c} {{\mathbf{r}}_d } \\ {{\mathbf{r}}_m } \\ \par \end{array} } \right],$](img14.png)
![$\displaystyle \Delta {\mathbf{p}}_{{\text{good}}} = [\begin{array}{*{20}c} {({\...
...}{*{20}c} {{\mathbf{r}}_d } \\ {{\mathbf{r}}_m } \\ \par \end{array} } \right].$](img15.png)
![]() , but that we use a search direction that is a gradient
with respect to
, but that we use a search direction that is a gradient
with respect to
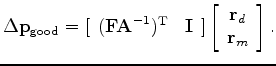 , not
, not
![]() . Using
. Using
![]() we have
we have
![]() . This enables us to define a good
search direction in model space:
. This enables us to define a good
search direction in model space:
![]() and notice that
and notice that
![]() .
.
![]() is equivalent to solving a
conjugate-gradient problem in
is equivalent to solving a
conjugate-gradient problem in
![]() .
.