Migration velocity analysis based on linearization of the two-way wave equation

Theory

First, we start with the imaging condition as the following:

$$I(\mathbf x, \mathbf h) = \sum_{\omega,\mathbf x_s,\mathbf x_r} G... ...^*(\mathbf x + \mathbf h,\mathbf x_r,\omega) d(\mathbf x_r,\mathbf x_s,\omega),$$ (1)

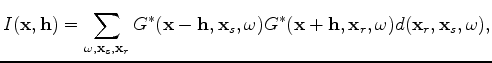where $I$ is the image, $G$ is the Green's function, $d$ is the surface data, $\mathbf x_s$ and $\mathbf x_r$ are the source and receiver coordinates, $\mathbf h$ is the subsurface offset, $\mathbf x$ is the Green's functions' coordinate and $\omega$ is frequency. Next, we define the Green's functions based on the two-way wave equation as follows:

$$\left( \nabla^2 + \omega^2 s^2(\mathbf x) \right) G(\mathbf x,\mathbf x_s,\omega)=-\delta(\mathbf x-\mathbf x_s),$$ (2)

$$\left( \nabla^2 + \omega^2 s^2(\mathbf x) \right) G(\mathbf x,\mathbf x_r,\omega)=-\delta(\mathbf x-\mathbf x_r),$$ (3)

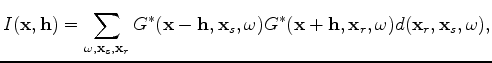where $s$ is slowness. Then, we can obtain the derivative of $I$ with respect to the slowness as follows;

$$\frac{\partial I(\mathbf x, \mathbf h)}{\partial s(\mathbf y)} = \sum_{\omega,\mathbf x_s,\mathbf x_r} \left( \frac{\partial G(\... ...G^*(\mathbf x + \mathbf h,\mathbf x_r,\omega) d(\mathbf x_r,\mathbf x_s,\omega)$$

$$+ \sum_{\omega,\mathbf x_s,\mathbf x_r} G^*(\mathbf x - \mathbf h... ..._r,\omega)}{\partial s(\mathbf y)} \right)^* d(\mathbf x_r,\mathbf x_s,\omega),$$ (4)

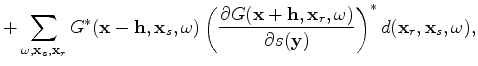where $\mathbf y$ is the slowness coordinate. Now, we can perturb the slowness:

$$s(\mathbf x) = s_0(\mathbf x) + \Delta s(\mathbf x),$$ (5)

where $s_0$ is the background slowness. Then, we apply a first order approximation by squaring the slowness and ignoring the second order perturbation term as follows:

$$s^2(\mathbf x) \approx s_0^2(\mathbf x) + 2 s_0(\mathbf x) \Delta s(\mathbf x).$$ (6)

We define a background Green's function that corresponds to the background slowness:

$$\left( \nabla^2 + \omega^2 s_0^2(\mathbf x \right) G_0(\mathbf x,\mathbf x_s,\omega)=-\delta(\mathbf x-\mathbf x_s).$$ (7)

By substituting this into the original wave equation, we arrive at the following:

$$\left( \nabla^2 + \omega^2 s_0^2(\mathbf x) \right) G(\mathbf x,\... ...a s(\mathbf x) G(\mathbf x,\mathbf x_s,\omega) - \delta(\mathbf x-\mathbf x_s).$$ (8)

Now, we apply Born's approximation to simplify the previous equation to the following expression:

$$\left( \nabla^2 + \omega^2 s_0^2(\mathbf x \right) \Delta G(\math... ... \omega^2 s_0(\mathbf x) \Delta s(\mathbf x) G_0(\mathbf x,\mathbf x_s,\omega),$$ (9)

where $\Delta G$ is the perturbed Green's function. Then, we solve for the perturbed Green's function as follows:

$$\Delta G(\mathbf x,\mathbf x_s,\omega)=-2 \omega^2 \sum_{\mathbf ... ...thbf y,\mathbf x_s,\omega) \Delta s(\mathbf y) G_0(\mathbf x,\mathbf y,\omega),$$ (10)

which enables us to find the derivative of the Green's function with respect to slowness as shown in the following:

$$\frac{\partial G(\mathbf x,\mathbf x_s,\omega)}{\partial s(\mathb... ...0(\mathbf y) G_0(\mathbf y,\mathbf x_s,\omega) G_0(\mathbf x,\mathbf y,\omega).$$ (11)

We can follow the same steps for the receiver Green's function to get:

$$\frac{\partial G(\mathbf x,\mathbf x_r,\omega)}{\partial s(\mathb... ...0(\mathbf y) G_0(\mathbf y,\mathbf x_r,\omega) G_0(\mathbf x,\mathbf y,\omega),$$ (12)

Then, we substitute equations (11) and (12) in the image derivative to get the result:

$$\frac{\partial I(\mathbf x, \mathbf h)}{\partial s(\mathbf y)}\vert_{s_0} =$$

$$\sum_{\omega,\mathbf x_s,\mathbf x_r} \left\lbrace-2 \omega^2 s_0... ...0^*(\mathbf x + \mathbf h,\mathbf x_r,\omega) d(\mathbf x_r,\mathbf x_s,\omega)$$

$$+ \sum_{\omega,\mathbf x_s,\mathbf x_r} \left\lbrace-2 \omega^2 s_0... ...t\rbrace G_0^*(\mathbf y,\mathbf x_r,\omega) d(\mathbf x_r,\mathbf x_s,\omega).$$ (13)

Finally, we can express the image perturbation as the following:

$$\Delta I(\mathbf x, \mathbf h) = \sum_{\mathbf y} \frac{\partial I(\mathbf x, \mathbf h)}{\partial s(\mathbf y)} \Delta s(\mathbf y)$$

$$= \sum_{\omega,\mathbf x_s,\mathbf x_r,\mathbf y} \left\lbrace-2 ... ...hbf h,\mathbf x_r,\omega) d(\mathbf x_r,\mathbf x_s,\omega) \Delta s(\mathbf y)$$

$$+ \sum_{\omega,\mathbf x_s,\mathbf x_r,\mathbf y} \left\lbrace-2 ... ...bf y,\mathbf x_r,\omega) d(\mathbf x_r,\mathbf x_s,\omega) \Delta s(\mathbf y),$$ (14)

Similarly, we can now compute the gradient, as given by:

$$\Delta s(\mathbf y) = \sum_{\mathbf x,\mathbf h} \left( \frac{\pa... ... h)}{\partial s(\mathbf y)}\vert_{s_0} \right)^* \Delta I(\mathbf x, \mathbf h)$$

$$= \sum_{\omega ,\mathbf x_s,\mathbf x_r,\mathbf x,\mathbf h} \lef... ... x_r,\omega) d^*(\mathbf x_r,\mathbf x_s,\omega) \Delta I(\mathbf x, \mathbf h)$$

$$+ \sum_{\omega ,\mathbf x_s,\mathbf x_r,\mathbf x,\mathbf h} \lef... ... x_r,\omega) d^*(\mathbf x_r,\mathbf x_s,\omega) \Delta I(\mathbf x, \mathbf h)$$

$$= -2 \omega^2 s_0(\mathbf y) \sum_{\omega ,\mathbf x_s,\mathbf x_... ...a) G_0(\mathbf x + \mathbf h,\mathbf x_r,\omega) \Delta I(\mathbf x, \mathbf h)$$

$$-2 \omega^2 s_0(\mathbf y) \sum_{\omega ,\mathbf x_s,\mathbf x_r}... ...) G_0(\mathbf x - \mathbf h,\mathbf x_s,\omega) \Delta I(\mathbf x, \mathbf h).$$ (15)

Migration velocity analysis based on linearization of the two-way wave equation