Implicit finite difference in time-space domain with the helix transform

Stability analysis

The Von-Neumann stability analysis is useful in predicting the largest time steps possible for a particular order of a finite-difference scheme, for which the wavefield will not diverge. The application of this analysis to the 2nd order in time and space explicit finite-difference approximation of the 2-way wave equation follows. Assuming $h = \Delta x = \Delta z$ , and using $t$ as a time index, the approximation is:

$$U_{hj,hl}^{t+1} = 2U_{hj,hl}^{t} - U_{hj,hl}^{t-1} + \frac{C^2 \D... ...),hl}^t + U_{h(j-1),hl}^t + U_{hj,h(l+1)}^t + U_{hj,h(l-1)}^t - 4 U_{hj,hl}^t).$$ (19)

The field being propagated is some function of time combined with a harmonic function of space:

$$U^t = F^t e^{i(k_x h j + k_z h l)}.$$ (20)

inserting 20 into 19 and then dividing by $e^{i(k_x h j + k_z h l)}$ yields:

$$F^{t+1} = 2F^t - F^{t-1} + \alpha \left( F^t e^{i k_x h} + F^t e^{-i k_x h} + F^t e^{i k_z h} + F^t e^{-i k_z h} - 4 \right),$$ (21)

where $\alpha = \frac{c^2 \Delta t^2}{h^2}.$

In order to have stable propagation, the amplification factor - the amplitude ratio between the future wavefield and the current wavefield, must be smaller or equal to 1. This is also a requirement for the ratio between the past wavefield and the current wavefield, as the time reversed wavefield must also remain stable. From this consideration we have:

$$\frac{F^{t+1}}{F^t} = \frac{F^{t-1}}{F^t} = g(k_x, k_z).$$ (22)

Dividing (21) by 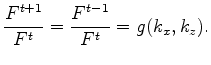$F^t$ , and using the trigonometric identity for cosine we get:

$$g(k_x, k_z) = 1 + \alpha \left( cos(k_x h) + cos(k_z h) - 2 \right) = 1 + \alpha R.$$ (23)

$R$ is bounded by $-4 \leq R \leq 0$ , and the requirement is that the amplification factor $\vert g\vert \leq 1$ . It follows that

$$1 - 4 \alpha \leq g \leq 1,$$

$$\vert 1 - 4 \alpha\vert \leq 1,$$

$$\alpha \leq \frac{1}{2}.$$ (24)

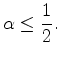Since $\alpha = \frac{C^2 \Delta t^2}{h^2}$ , this analysis provides us with a way to determine the maximum time step for a given minimum velocity and spatial differencing step.
The same derivation for the 2D implicit finite differencing weights as derived in Equation 17 yields the amplification factor:

$$g(k_x, k_z) = \frac{1 + \alpha R}{1 - 2 \alpha R}.$$ (25)

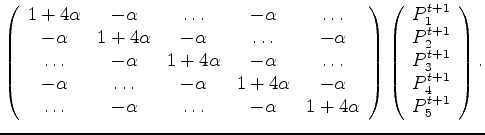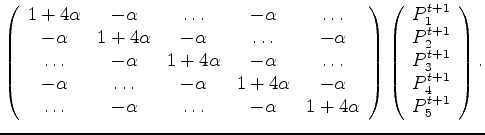The boundaries for $R$ remain $-4 \leq R \leq 0$ . Because $\alpha$ is necessarily positive, it follows that $\vert g\vert \leq 1$ for any $\alpha$ in this 2D implicit finite-difference scheme. The time step can be arbitrarily large without causing the wavefield to diverge. This, of course, does not mean that we will get a 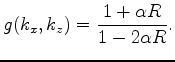$useful$ wavefield with any arbitrary $\Delta t$ .

Implicit finite difference in time-space domain with the helix transform