|
|
|
|
Wave-equation traveltime tomography by global optimization |
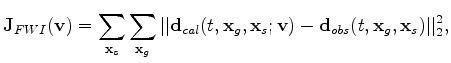 and
and 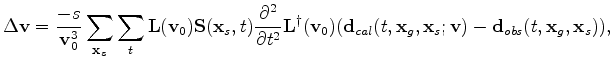 is the step size,
is the step size, The objective function wave-equation traveltime tomography can be written as follows:
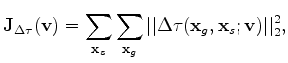 is the lag of the maximum cross-correlation between the observed data and the data modeled by a velocity model
is the lag of the maximum cross-correlation between the observed data and the data modeled by a velocity model 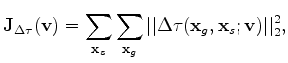 is set to zero to get the velocity update, which can be expressed as follows:
is set to zero to get the velocity update, which can be expressed as follows:
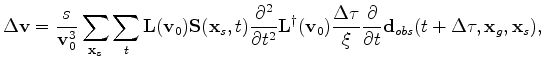 is defined as follows:
is defined as follows:
Now, I cast the picking procedure of the lags
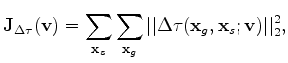 as a global optimization problem with an objective function as follows:
as a global optimization problem with an objective function as follows:
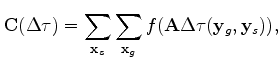 and
and
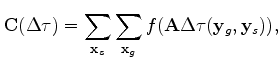 and
and
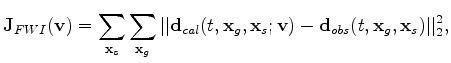 , and
, and The goal of the global optimization is to maximize the function described by equation (6), which is to maximize the stacking power along the interpolated spline surface. The searching procedure is a simulated annealing algorithm, which varies the spline points along the time axis in a stochastic sense until a satisfying solution is reached. In the following section, I show the results of using such global scheme to pick the correlation lags.
|
|---|
|
velali
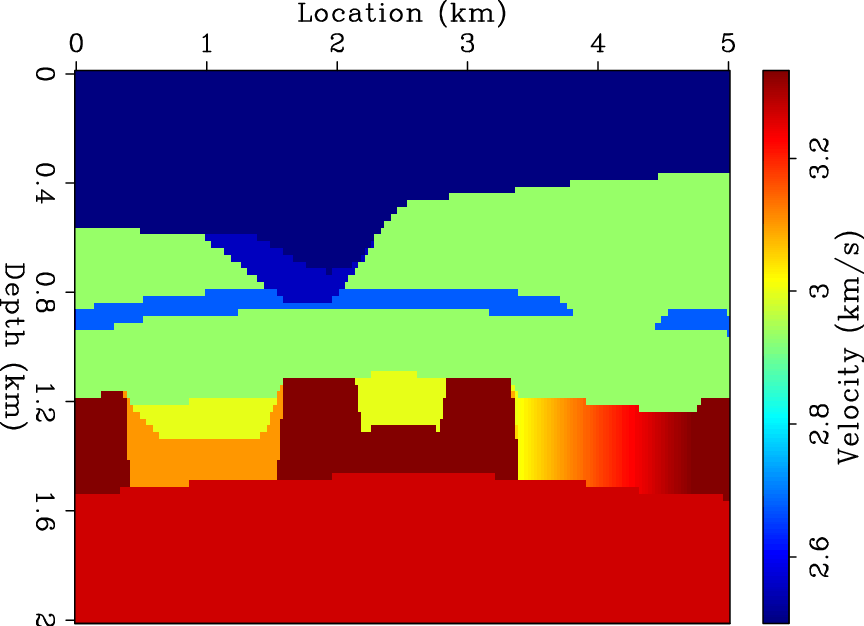
Figure 1. The true velocity model used to create the data. |
|
|
|
|
|
|
Wave-equation traveltime tomography by global optimization |