|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |
At this point I have determined a data processing scheme that would provide all the drained
constants for a poroelasticity system from measurements of the undrained constants.
In the example of the preceding subsection, I needed to broaden the meaning of the undrained set of constants
to include the Skempton 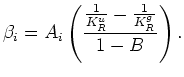 coefficients, which were not needed in earlier parts of the paper.
But they could nevertheless be computed from the information found earlier,
since I did show how to compute all the
coefficients, which were not needed in earlier parts of the paper.
But they could nevertheless be computed from the information found earlier,
since I did show how to compute all the ![]() 's directly, and these coefficients
provide just the information that I would need for determining these values from (57).
's directly, and these coefficients
provide just the information that I would need for determining these values from (57).
In realistic data collection situations, especially those involving field data, my previous assumptions concerning the nature and orientations of the constituent grains of the granular porous medium may sometimes - perhaps most times - be too idealized. Nevertheless, it is the case that the equations of poroelasticity never become any more complex than those shown here. What does change is the interpretation of the directional grain moduli. In the worst case scenario, equation (60) needs to be replaced by an equation of the same form, namely:
To provide different ideas about how important the anisotropy, and the random orientation of the constituents might be in a few cases, TABLES 1 and 2 show some quantitative examples based on results of Berryman (2005) and Ranganathan and Ostoja-Starzewski (2008a,b). TABLES 3 and 4, respectively, provide input data for the types of orthorhombic solids (Musgrave, 2003), and the results for the Voigt, Reuss, and directional measures of bulk moduli for these particular materials. Note the significant finding that the directional moduli do not have to stay within the values set by the Voigt and Reuss estimators.
Tables 5-9 show similar results for selected data taken from the compendium assembled by Simmons and Wang (1971).
1.2
| Stiffness | Aluminum (Al) | Copper (Cu) | Magnesia (MgO) | Spinel
(MgAl |
|
| 107.30 | 170.98 | 297.08 | 298.57 | ||
| 60.80 | 123.99 | 95.36 | 153.72 | ||
| 28.30 | 75.45 | 156.13 | 157.58 |
1.2
| Bulk Modulus | Al | Cu | MgO | MgAl |
|
|
76.3 | 139.65 | 162.6 | 202.00 |
|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |