The inverse problem for imaging multiples using up- and down-going data

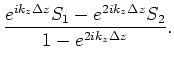The inverse problem for imaging multiples using up- and down-going data can be fomulated as follow. We first break down the recorded data as the superposition of up- $\bold d_{\uparrow}$ and down-going $\bold d_{\downarrow}$ signals at the receivers. This can be done by using PZ data to give up-going and down-going data as discussed in the PZ summation section above.

$\displaystyle \left[ \begin{array}{c} \bold d_{\uparrow} \\ \bold d_{\downarro... ..._{pz} \left[ \begin{array}{c} \bold d_{p} \\ \bold d_{z} \end{array} \right]$

The above construction assumes that the vertical particle velocity 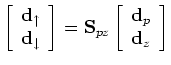$ d_z$

contains mostly pressure ( $\bold P$ ) waves. A pre-processing step can be included into $\bold S_{pz}$ to separate the $\bold P-$ and converted $\bold S-$ wave arrivals (Helbig and Mesdag, 1982; Dankbaar, 1985). Next, we denote the modelling operator for up-going signals at the receivers as $\bold L_{\uparrow}$ . Similarily, denote the modeling operator for down-going signals at the receivers as $\bold L_{\downarrow}$ . The two modeling operators provide the up- and down-going modeled data, denoted as $\bold d^{mod}_{\uparrow}$ and $\bold d^{mod}_{\downarrow}$ ;

$\displaystyle \bold d^{mod}_{\uparrow}$	$\displaystyle =$	$\displaystyle \bold L_{\uparrow} \bold m ,$
$\displaystyle \bold d^{mod}_{\downarrow}$	$\displaystyle =$	$\displaystyle \bold L_{\downarrow} \bold m .$	(5)

The inverse problem is defined as minimizing the

norm of the two data residuals $\bold r_{\uparrow}$ and $\bold r_{\downarrow}$ , with respect to a single model $\bold m$ . The data residuals are defined as the difference between the recorded data and the modelled data,

$\displaystyle \bold r_{\uparrow}$	$\displaystyle =$	$\displaystyle \bold d_{\uparrow} - \bold d^{mod}_{\uparrow} = \bold d_{\uparrow} - \bold L_{\uparrow} \bold m ,$
$\displaystyle \bold r_{\downarrow}$	$\displaystyle =$	$\displaystyle \bold d_{\downarrow} - \bold d^{mod}_{\downarrow} = \bold d_{\downarrow} - \bold L_{\downarrow} \bold m ,$	(6)

$\displaystyle min \left( \Vert \bold L_{\uparrow} \bold m - \bold d_{\uparrow} ... ...+ \Vert \bold L_{\downarrow} \bold m - \bold d_{\downarrow} \Vert _2^2 \right),$

(7)

where $\Vert . \Vert _{2}$ represents the

norm. In matrix form, the fitting goal can be written as

$\displaystyle 0 \approx \left[ \begin{array}{c} \bold L_{\uparrow} \\ \bold L_... ...in{array}{c} \bold d_{\uparrow} \\ \bold d_{\downarrow} \end{array} \right].$

With the conjugate gradient method, the model update 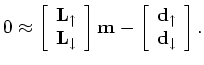$\Delta \bold m$ at each iteration has contributions from both the up-going and down-going parts of the inversion;

$\displaystyle \Delta \bold m = \bold L'_{\uparrow} \bold r_{\uparrow} + \bold L'_{\downarrow} \bold r_{\downarrow}.$

(8)

where $\bold r_{\uparrow} = \bold L_{\uparrow} \bold m - \bold d_{\uparrow}$ and $\bold r_{\downarrow} = \bold L_{\downarrow} \bold m - \bold d_{\downarrow}$ is the up- and down-going part of the residual, respectively.

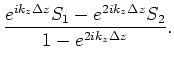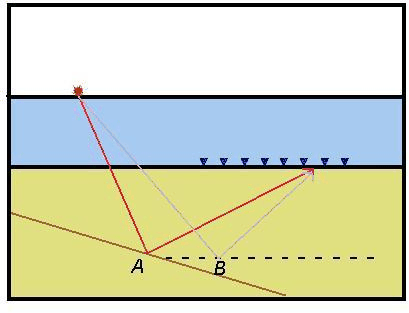
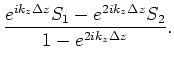The justification for this inverse problem is to reduce the wrong placement of image point with the use of both $\bold d_{\uparrow}$ and $\bold d_{\downarrow}$ signals. Traditional migration scheme only uses $d_{\uparrow}$ to determine the image since all primary signal can be found in $\bold d_{\uparrow}$ . However, migration of primaries can give incorrect image point as well. In Figure 4, a primary event with a given travel time can indicate a correct image point at A and an incorrect image point at B. If we include the previously ignored information $\bold d_{\downarrow}$ into a joint inversion, some wrongly placed image point can be refuted. Joint imaging allow us to use both primaries and multiples to estimate the image. This can be a distinct advantage because multiples and primaries illuminate different parts of the sub-surface. For ocean bottom data with sparse receiver spacing, multiples illuminate more than primaries.

The quality of the inverse problem would depend on the implemetation of the modeling operator. The next section will discuss how to approximate the modeling operator.