Measuring image focusing for velocity analysis

Image curvature and residual migration

In presence of point diffractors, the semblance functional defined in expression 1 yields unbiased estimates of the velocity parameter $\rho$. However, when the curvature is finite, the dip components would not be aligned for the correct value of $\rho$ and the estimates would be biased. To remove this bias we can correct the dip-decomposed images for the presence of curvature. In Appendix A I show the simple derivation of this correction that amounts to the following spatial shift, $\Delta{{\bf n}}_{\rm Curv}$, along the normal to the structural dip,

$$\Delta{{\bf n}}_{\rm Curv}= \frac {\sin\left(\alpha -\bar{\alpha}\right) \tan\left(\alpha -\bar{\alpha}\right)} {2} {R}{\bf n},$$ (A-2)

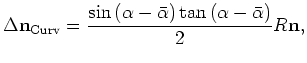where ${R}$ is the local radius of curvature, $\bar{\alpha}$ is the local dip and 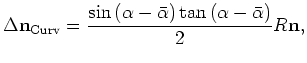${\bf n}$ is the vector normal to the dip $\alpha$ and directed towards increasing depth. Notice that the application of this correction requires the estimation of local dip $\bar{\alpha}$. To estimate the local dips, I used the Seplib program Sdip that implements a variant of the algorithms described by Fomel (2002).

Expression 2 can be used directly to create an ensemble to dip-decomposed images that are corrected for the local curvature ${\bf R}_{{\rm Curv}}\left({\bf x},\gamma ,\alpha ,\rho,{R}\right)$. The image-focusing semblance can be computed on these images as:

$$S_{\left(\gamma ,\alpha \right)}\left({\bf x},\rho,{R}\right)= \f... ...m_\alpha {\bf R}_{{\rm Curv}}\left({\bf x},\gamma ,\alpha ,\rho,{R}\right)^2 }.$$ (A-3)

However, the application of correction 2 can be quite expensive unless it is performed together with residual migration. Furthermore, precomputing the curvature-corrected images would further increase the dimensionality of the image space, creating obvious problems for handling the resulting bulky data sets. Fortunately, when the ensemble of the dip-decomposed images ${\bf R}\left({\bf x},\gamma ,\alpha ,\rho\right)$ are the result of residual prestack migration, the curvature correction can be efficiently computed during the evaluation of the semblance functional 3. Correction 2 becomes a simple interpolation along the residual velocity parameter $\rho$, as a function of the aperture angles and dips.

To derive the interpolating function, I first recall the expression of residual migration in Biondi (2008a):

$$\Delta{{\bf n}}_{\rm Rmig}= \left(\rho_{\rm new}-\rho_{\rm old}\right) \frac{\cos \alpha } {\left(cos^2\alpha -\sin^2\gamma \right)} z_{0}{\bf n},$$ (A-4)

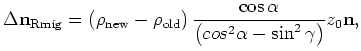where $\Delta{{\bf n}}_{\rm Rmig}$ is the normal shift applied by residual migration, $\rho_{\rm new}$ is the value of $\rho$ after residual migration and $\rho_{\rm old}$ is the value of $\rho$ before residual migration, which is usually set to be equal to one. The parameter $z_{0}$ is a constant that is equal to the depth for which the residual migration in 4 is exact.

Equating the normal shift in 4 with the normal shift in 2 and solving for $\rho_{\rm new}$ we obtain

$$\rho_{\rm new}= \rho_{\rm old} +\frac {\sin\left(\alpha -\bar{\al... ...lpha}\right)\left(\cos^2\alpha -\sin^2\gamma \right)} {2 \cos\alpha z_{0}} {R}.$$ (A-5)

In this case, $\rho_{\rm new}$ is the $\rho$ of the images from which the data are interpolated from, and $\rho_{\rm old}$ is the $\rho$ of the images after correction; that is,

$${\bf R}_{{\rm Curv}}\left({\bf x},\gamma ,\alpha ,\rho_{\rm old},... ...o_{\rm new}\left(\rho_{\rm old},\gamma ,\alpha ,\bar{\alpha},{R}\right)\right].$$ (A-6)

Measuring image focusing for velocity analysis