Measuring image focusing for velocity analysis

Image curvature and residual migration in the pseudo-depth domain

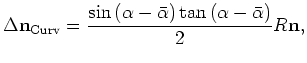The interpolation defined by 5 depends in a non-straightforward manner from both angles $\gamma$ and $\alpha$, as well as from the estimate of the local dip $\bar{\alpha}$. Although, this is the relationship I used in practice for the examples in this paper, I will now analyze one of its variants that is simpler and thus it helps to better understand the relationship between image curvature and residual migration parameter.

I start from redefining residual migration in the pseudo-depth domain $\tilde{z}=z/\rho$ (Sava, 2004). In this domain, the focusing/unfocusing effects of residual migration are better separated from its mapping effects than in the conventional depth domain. In the pseudo-depth domain, normal-incidence images of flat reflectors are not shifted by residual migration. The expression of residual migration 4 becomes:

$$\Delta{{\bf n}}_{\rm Rmig}= \left(\rho_{\rm new}-\rho_{\rm old}\r... ... } {\left(\cos^2\alpha -\sin^2\gamma \right)} -\cos\alpha \right] z_{0}{\bf n},$$ (A-7)

and the expression of curvature correction 5 becomes:

$$\rho_{\rm new}= \rho_{\rm old} +\frac {\sin^{2}\left(\alpha -\bar... ...a -\bar{\alpha}\right)\cos\alpha \left(\sin^2\alpha +\sin^2\gamma \right)} {R},$$ (A-8)

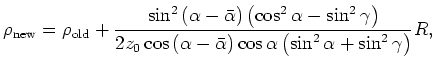that also does not provide a straightforward relationship between the input and output $\rho$s. Furthermore, it becomes singular for the flat dip component ($\alpha =0$) of normal incidence images ($\gamma =0$). Its use is thus more cumbersome than the use the equivalent expression in the depth domain (equation 5).

However, in the special case of events that are locally flat ( $\bar{\alpha}=0$) and are imaged at normal-incidence (i.e. $\gamma =0$), this expression simplifies into:

$$\rho_{\rm new}= \rho_{\rm old} +\frac {{R}}{2 z_{0}}.$$ (A-9)

In this case, the curvature correction becomes independent from the dip $\alpha$. It only remaps the image from $\rho_{\rm new}$ to $\rho_{\rm old}$ and thus does not affect the coherency along the dip direction of the dip-decomposed images. There is perfect ambiguity between the residual migration parameter $\rho$ and the reflector radius of curvature ${R}$.

Measuring image focusing for velocity analysis