 |
 |
 |
 | Measuring image focusing for velocity analysis |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Biondi: Image-focusing analysis
Previous: APPENDIX A
This appendix derives the expression for the curvature
correction presented in the main text in 2.
The derivation is extremely simple and based on the geometry sketched in
Figure 21.
The reflector is approximated with a parabola with
radius of curvature 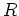 at its vertex.
In the rotated coordinates system
at its vertex.
In the rotated coordinates system
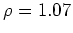 the equation of the parabola is
the equation of the parabola is
 |
(A-1) |
The shift 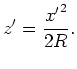 that moves a tangent to the parabola
to the vertex is equal to
that moves a tangent to the parabola
to the vertex is equal to
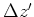 |
(A-2) |
and consequently the normal shift 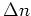 is equal to
is equal to
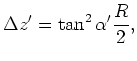 |
(A-3) |
The coordinate system
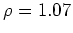 is rotated by
is rotated by
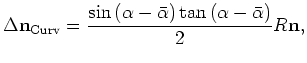 with respect to
with respect to
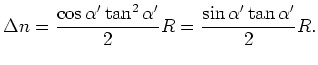 .
Removing that rotation is equivalent to set
.
Removing that rotation is equivalent to set
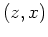 ;
performing this substitution in the previous equation, I obtain the correction
in 2; that is,
;
performing this substitution in the previous equation, I obtain the correction
in 2; that is,
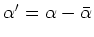 |
(A-4) |
Curv-corr
Figure 21.
Sketch used to derive the curvature correction
presented in 2.
The tangent to the parabola (dashed line) needs to be shifted by 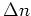 to pass through the vertex of the parabola.
[NR]
to pass through the vertex of the parabola.
[NR]
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
 |
 |
 |
 | Measuring image focusing for velocity analysis |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Biondi: Image-focusing analysis
Previous: APPENDIX A
2009-05-05
![]() at its vertex.
In the rotated coordinates system
at its vertex.
In the rotated coordinates system
![]() the equation of the parabola is
the equation of the parabola is
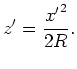 that moves a tangent to the parabola
to the vertex is equal to
that moves a tangent to the parabola
to the vertex is equal to
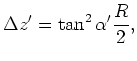
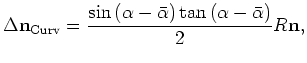 with respect to
with respect to
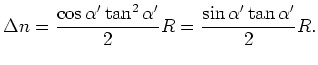 .
Removing that rotation is equivalent to set
.
Removing that rotation is equivalent to set
