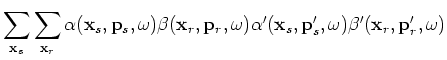|
 |
 |
 | Modeling, migration, and inversion in the generalized source and receiver domain |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Modeling, migration, and inversion
Previous: APPENDIX B
This appendix derives the objective function in the simultaneously encoded source and receiver domain.
We start with the objective function in the source and receiver domain as follows:
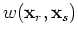 |
|
|
(C-1) |
If we follow a discussion similar to those in Appendices A and B, we obtain the general expression of the inverse transform of the simultaneous encoding:
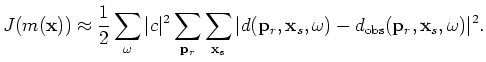 |
|
|
(C-2) |
Substituting Equation C-2 into C-1 yields:
where
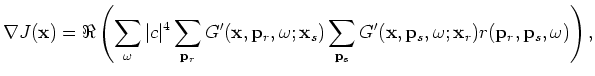 is defined to be the residual in the encoded source and receiver domain:
is defined to be the residual in the encoded source and receiver domain:
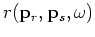 |
|
|
(C-4) |
For plane-wave phase encoding, with sampling dense enough in 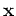 and
and 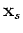 , the inner-most summations become Dirac delta functions:
, the inner-most summations become Dirac delta functions:
| |
|
 |
|
| |
|
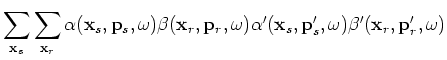 |
(C-5) |
For random phase encoding, we can also approximately have
| |
|
 |
|
| |
|
 |
(C-6) |
Therefore the data-misfit function in the encoded source and receiver domain is
 |
|
|
(C-7) |
 |
 |
 |
 | Modeling, migration, and inversion in the generalized source and receiver domain |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Modeling, migration, and inversion
Previous: APPENDIX B
2009-04-13

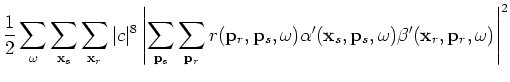
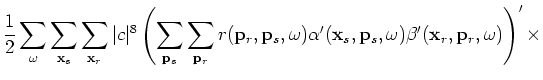


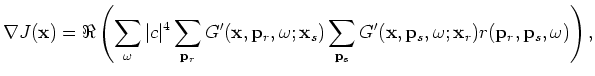 is defined to be the residual in the encoded source and receiver domain:
is defined to be the residual in the encoded source and receiver domain:
![]() and
and ![]() , the inner-most summations become Dirac delta functions:
, the inner-most summations become Dirac delta functions: