 |
 |
 |
 | Image-space wave-equation tomography in the generalized source domain |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Image-space wave-equation tomography in
Previous: APPENDIX B
This appendix demonstrates a matrix representation of the adjoint tomographic operator
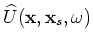 .
Since the slowness perturbation
.
Since the slowness perturbation
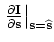 is linearly related to the perturbed wavefields,
is linearly related to the perturbed wavefields,
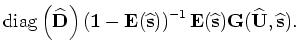 and
and
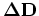 ,
to obtain the back-projected slowness perturbation, we first must get the back-projected perturbed wavefields from the perturbed image
,
to obtain the back-projected slowness perturbation, we first must get the back-projected perturbed wavefields from the perturbed image
 .
From Equation B-15, the back-projected perturbed source and receiver wavefields are obtained as follows:
.
From Equation B-15, the back-projected perturbed source and receiver wavefields are obtained as follows:
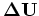 |
|
|
(C-1) |
and
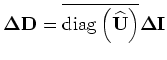 |
|
|
(C-2) |
Then the adjoint equations of Equations B-10 and B-14 are
used to get the back-projected slowness perturbation
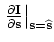 .
Let us first look at the adjoint equation of Equation B-10, which can be written as follows:
.
Let us first look at the adjoint equation of Equation B-10, which can be written as follows:
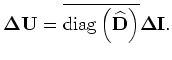 |
|
|
(C-3) |
We can define a temporary wavefield
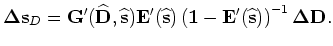 that satisfies the following equation:
that satisfies the following equation:
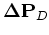 |
|
|
(C-4) |
After some simple algebra, the above equation can be rewritten as follows:
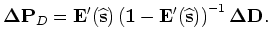 |
|
|
(C-5) |
Substituting Equation C-1 into equation C-5 yields
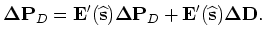 |
|
|
(C-6) |
Therefore,
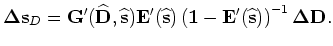 can be obtained by recursive upward continuation,
where
can be obtained by recursive upward continuation,
where
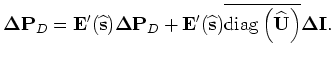 serves as the initial condition.
The back-projected slowness perturbation from the perturbed source wavefield is then obtained by applying the adjoint of the scattering
operator
serves as the initial condition.
The back-projected slowness perturbation from the perturbed source wavefield is then obtained by applying the adjoint of the scattering
operator
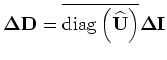 to the wavefield
to the wavefield
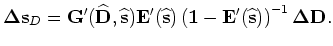 as follows:
as follows:
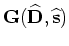 |
|
|
(C-7) |
Similarly, the adjoint equation of Equation B-14 reads as follows:
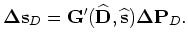 |
|
|
(C-8) |
We can also define a temporary wavefield
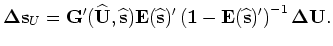 that satisfies the following equation:
that satisfies the following equation:
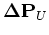 |
|
|
(C-9) |
After rewriting it, we get the following recursive form:
The back-projected slowness perturbation from the perturbed receiver wavefield is then obtained by applying the adjoint of
the scattering operator
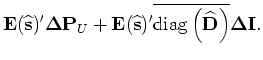 to the wavefield
to the wavefield
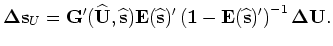 as follows:
as follows:
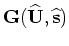 |
|
|
(C-11) |
The total back-projected slowness perturbation is obtained by adding
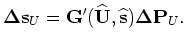 and
and
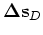 together:
together:
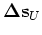 |
|
|
(C-12) |
 |
 |
 |
 | Image-space wave-equation tomography in the generalized source domain |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Image-space wave-equation tomography in
Previous: APPENDIX B
2009-04-13
![]() .
Since the slowness perturbation
.
Since the slowness perturbation
![]() is linearly related to the perturbed wavefields,
is linearly related to the perturbed wavefields,
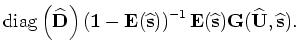 and
and
![]() ,
to obtain the back-projected slowness perturbation, we first must get the back-projected perturbed wavefields from the perturbed image
,
to obtain the back-projected slowness perturbation, we first must get the back-projected perturbed wavefields from the perturbed image
![]() .
From Equation B-15, the back-projected perturbed source and receiver wavefields are obtained as follows:
.
From Equation B-15, the back-projected perturbed source and receiver wavefields are obtained as follows:
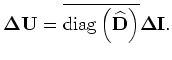
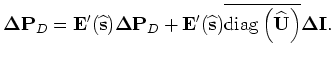 serves as the initial condition.
The back-projected slowness perturbation from the perturbed source wavefield is then obtained by applying the adjoint of the scattering
operator
serves as the initial condition.
The back-projected slowness perturbation from the perturbed source wavefield is then obtained by applying the adjoint of the scattering
operator
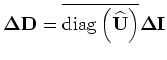 to the wavefield
to the wavefield
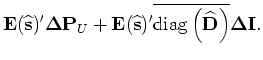 to the wavefield
to the wavefield