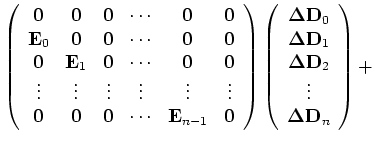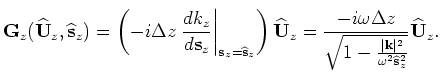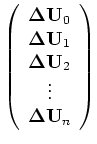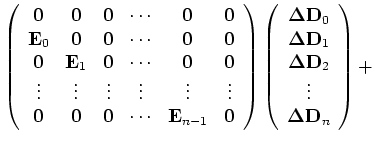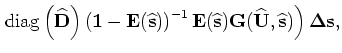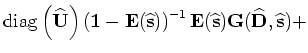|
 |
 |
 | Image-space wave-equation tomography in the generalized source domain |  |
![[pdf]](icons/pdf.png) |
Next: APPENDIX C
Up: Image-space wave-equation tomography in
Previous: APPENDIX A
This appendix demonstrates a matrix representation of the forward tomographic operator 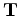 .
Let us start with the source wavefield, where the source wavefield
.
Let us start with the source wavefield, where the source wavefield 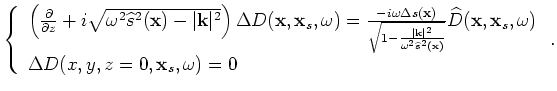 at depth
at depth  is downward continued to depth
is downward continued to depth
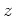 by the one-way extrapolator
by the one-way extrapolator
 as follows:
as follows:
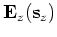 |
|
|
(B-1) |
where the one-way extrapolator is defined as follows:
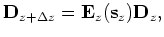 |
|
|
(B-2) |
The perturbed source wavefield at some depth level can be derived from the background wavefield by a simple
application of the chain rule to equation B-1:
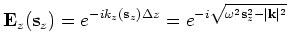 |
|
|
(B-3) |
where
 is the background source wavefield and
is the background source wavefield and
 represents the perturbed extrapolator,
which can be obtained by a formal linearization
with respect to slowness of the extrapolator defined in Equation B-2:
represents the perturbed extrapolator,
which can be obtained by a formal linearization
with respect to slowness of the extrapolator defined in Equation B-2:
where
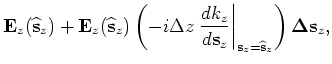 and
and
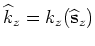 is the background slowness at depth
is the background slowness at depth  .
From Equation B-4, the perturbed extrapolator reads as follows:
.
From Equation B-4, the perturbed extrapolator reads as follows:
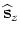 |
|
|
(B-5) |
Substituting Equation B-5 into B-3 yields
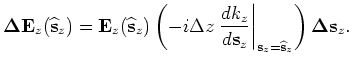 |
|
|
(B-6) |
Let us define a scattering operator 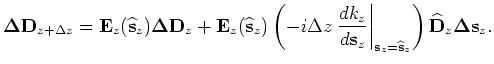 that interacts with the background wavefield as follows:
that interacts with the background wavefield as follows:
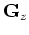 |
|
|
(B-7) |
Then the perturbed source wavefield for depth
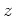 can be rewritten as follows:
can be rewritten as follows:
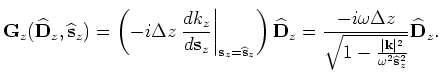 |
|
|
(B-8) |
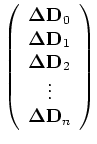
We can further write out the recursive Equation B-8 for all depths in the following matrix form:
or in a more compact notation,
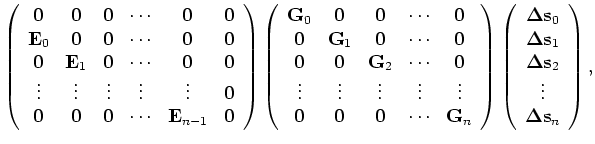 |
|
|
(B-9) |
The solution of Equation B-9 can be formally written as follows:
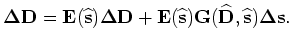 |
|
|
(B-10) |
Similarly, the perturbed receiver wavefield satisfies the following recursive relation:
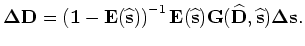 |
|
|
(B-11) |
where
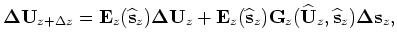 is the scattering operator, which interacts with the background receiver wavefield as follows:
is the scattering operator, which interacts with the background receiver wavefield as follows:
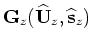 |
|
|
(B-12) |
We can also write out the recursive Equation B-12 for all depth levels in the following matrix form:
or in a more compact notation,
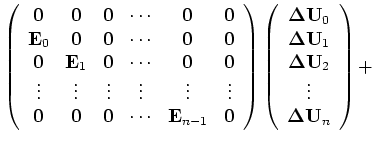 |
|
|
(B-13) |
The solution of Equation B-13 can be formally written as follows:
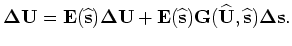 |
|
|
(B-14) |
With the background wavefields and the perturbed wavefields, the perturbed image can be obtained as follows:
or in a more compact notation,
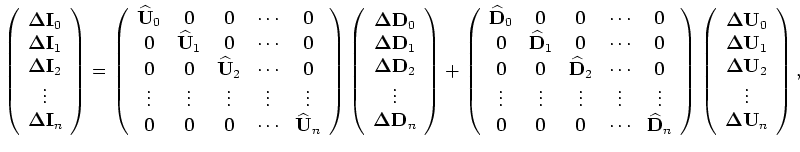 |
|
|
(B-15) |
Substituting Equations B-10 and B-14 into Equation B-15 yields
from which we can read the forward tomographic operator 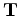 as follows:
as follows:
 |
 |
 |
 | Image-space wave-equation tomography in the generalized source domain |  |
![[pdf]](icons/pdf.png) |
Next: APPENDIX C
Up: Image-space wave-equation tomography in
Previous: APPENDIX A
2009-04-13
![]() .
Let us start with the source wavefield, where the source wavefield
.
Let us start with the source wavefield, where the source wavefield 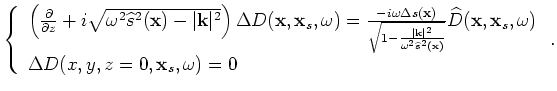 at depth
at depth ![]() is downward continued to depth
is downward continued to depth
![]() by the one-way extrapolator
by the one-way extrapolator
![]() as follows:
as follows:
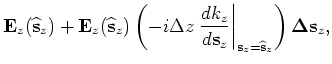 and
and
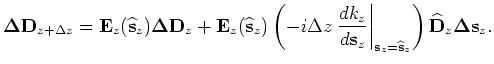 that interacts with the background wavefield as follows:
that interacts with the background wavefield as follows: