|
|
|
|
Plane-wave migration in tilted coordinates |
|
zigvelwithraytilt
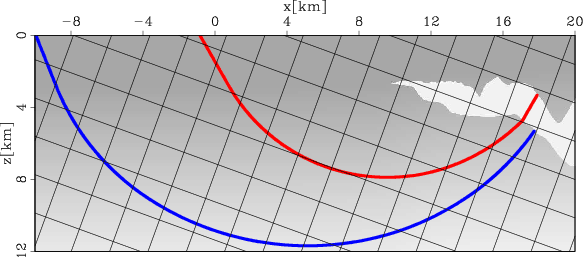
Figure 4. The velocity model and overturned waves in a tilted coordinate system. The overturned waves in vertical Cartesian coordinates do not overturn in the tilted coordinate system. |
|
|---|---|
|
|
Waves from a point source propagate radially, and waves start from one spatial location and travel along all directions.
Therefore, it is impossible for a tilted coordinate system to cover all the propagation directions of a point source.
Figure 5a illustrates the waves from a point source in tilted coordinates.
In Figure 5a the coordinates ![]() are rotated counter-clockwise, where the high-angle energy
can be well modeled on the right side, but the left-side energy (represented by dash-lines) cannot be modeled accurately,
even for small-angle energy in vertical Cartesian coordinates.
However, the propagation direction of a plane-wave source at different spatial locations is usually similar (Figure 5b).
In plane-wave migration, we decompose the wavefield into plane-wave source gathers by
slant-stacking, and each plane-wave source gather is characterized by a ray-parameter
are rotated counter-clockwise, where the high-angle energy
can be well modeled on the right side, but the left-side energy (represented by dash-lines) cannot be modeled accurately,
even for small-angle energy in vertical Cartesian coordinates.
However, the propagation direction of a plane-wave source at different spatial locations is usually similar (Figure 5b).
In plane-wave migration, we decompose the wavefield into plane-wave source gathers by
slant-stacking, and each plane-wave source gather is characterized by a ray-parameter ![]() .
Given the velocity at the surface
.
Given the velocity at the surface ![]() , the propagation direction of the plane-wave source
is defined by the vector
, the propagation direction of the plane-wave source
is defined by the vector ![]() , where
, where
![]() and
and
![]() .
Therefore, the ray parameter
.
Therefore, the ray parameter ![]() defines the propagation direction of the plane-wave source at the surface.
The take-off angle
defines the propagation direction of the plane-wave source at the surface.
The take-off angle ![]() of the plane-wave source can be calculated as follows:
of the plane-wave source can be calculated as follows:
| (15) |
|
pointplane
Figure 5. Point source (a) and plane-wave sources (b) in tilted coordinates. Waves from a point source propagate radially, and the waves represented by the dash line rays in panel (a) can not be caught when we rotate the coordinates counter-clockwise. In contrast, the propagation directions of the plane-wave source are similar in different spatial points, so most of them can be extrapolated accurately in a tilted coordinate system. |

|
|---|---|
|
|
Given a plane-wave source with a take-off angle of ![]() ,
we use tilted coordinates
,
we use tilted coordinates
![]() , with a tilting angle
, with a tilting angle 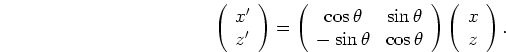 close to its take-off angle
close to its take-off angle ![]() .
Usually, velocity increases with depth and the propagation direction of waves becomes increasingly horizontal,
so in practice the tilting angle
.
Usually, velocity increases with depth and the propagation direction of waves becomes increasingly horizontal,
so in practice the tilting angle 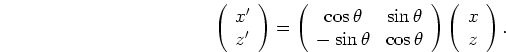 is a little larger than the take-off angle.
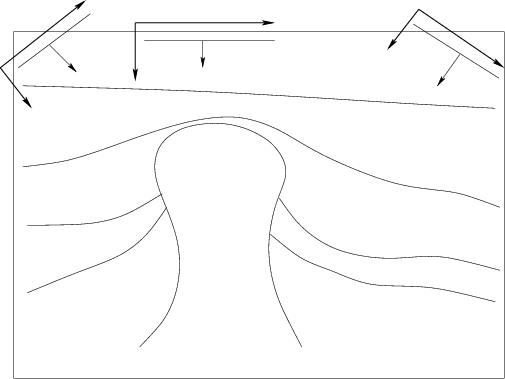
Figure 6 shows three typical plane-wave sources and their tilted coordinate systems.
Plane-wave sources with a small take-off angle mainly illuminate reflectors that are almost flat,
so we extrapolate wavefields vertically.
In contrast, plane-wave sources with a large take-off angle mainly illuminate steeply dipping reflectors,
so we use a tilted coordinate system with a large tilting angle.
Usually, these wavefields are difficult to extrapolate accurately by downward continuation migration,
but in tilted coordinates their propagation direction is close to the extrapolation direction, so
they can be imaged correctly. Waves overturning in vertical Cartesian coordinates do not overturn in a well-chosen tilted coordinate system.
Therefore, in plane-wave migration in tilted coordinates, each plane-wave source has its own tilted coordinate system in which the extrapolation direction
is close to the propagation direction, and steep reflectors and overturned waves can be imaged correctly.
is a little larger than the take-off angle.
Figure 6 shows three typical plane-wave sources and their tilted coordinate systems.
Plane-wave sources with a small take-off angle mainly illuminate reflectors that are almost flat,
so we extrapolate wavefields vertically.
In contrast, plane-wave sources with a large take-off angle mainly illuminate steeply dipping reflectors,
so we use a tilted coordinate system with a large tilting angle.
Usually, these wavefields are difficult to extrapolate accurately by downward continuation migration,
but in tilted coordinates their propagation direction is close to the extrapolation direction, so
they can be imaged correctly. Waves overturning in vertical Cartesian coordinates do not overturn in a well-chosen tilted coordinate system.
Therefore, in plane-wave migration in tilted coordinates, each plane-wave source has its own tilted coordinate system in which the extrapolation direction
is close to the propagation direction, and steep reflectors and overturned waves can be imaged correctly.
|
planetilt
Figure 6. Plane-wave sources and their tilted coordinates. The tilting direction for the coordinates corresponding to the plane-wave source depends on its take-off angle. There are three typical plane-wave sources, and they have 0, negative and positive ray parameters, respectively. For |
|
|---|---|
|
|
|
|---|
|
reciprocity
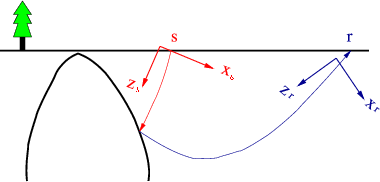
Figure 7. Reciprocity improves plane-wave migration in tilted coordinates. The source location is at |
|
|
Usually, in streamer acquisition we only record one-sided offset data at the surface. But we can obtain the data for the other side by reciprocity. Merging the original data and the data obtained by reciprocity, we obtain a dataset that would be recorded if we would have had a split-spread recording geometry. In plane-wave migration for a dataset with a split-spread geometry, the aperture of each plane-wave source is almost the same as one-sided offset dataset, and thus the computation cost is also almost the same. But a split-spread recording geometry improves the plane-wave gathers and the signal-to-noise ratio of the image (Liu et al., 2006).
Reciprocity yields other benefits for plane-wave migration in tilted coordinates.
Figure 7 illustrates how reciprocity helps to image steep salt flanks when
the source ray does not overturn but the receiver ray does. In Figure 7,
the source location is ![]() and receiver location is
and receiver location is ![]() . For the original data, we run plane-wave migration
for this event using the coordinates
. For the original data, we run plane-wave migration
for this event using the coordinates ![]() , whose tilting angle is determined by the source ray direction
at the surface. The source plane wave starts at the surface almost vertically, and the tilting angle of its corresponding coordinates
, whose tilting angle is determined by the source ray direction
at the surface. The source plane wave starts at the surface almost vertically, and the tilting angle of its corresponding coordinates ![]() is small. As a consequence, the overturned receiver wave
cannot be accurately modeled, and the event cannot be correctly imaged. Reciprocity exchanges the source
and receiver locations. For the data obtained by reciprocity, we run plane-wave migration for this event using the coordinates
is small. As a consequence, the overturned receiver wave
cannot be accurately modeled, and the event cannot be correctly imaged. Reciprocity exchanges the source
and receiver locations. For the data obtained by reciprocity, we run plane-wave migration for this event using the coordinates ![]() , whose direction is determined by the receiver ray direction at the surface.
In the coordinates
, whose direction is determined by the receiver ray direction at the surface.
In the coordinates ![]() , both source and receiver waves can be accurately modeled, and the overturned
energy can be correctly imaged. When we run plane-wave migration in tilted coordinates for a split-spread dataset,
we design the coordinates considering the direction of both the source and receiver waves at the surface.
, both source and receiver waves can be accurately modeled, and the overturned
energy can be correctly imaged. When we run plane-wave migration in tilted coordinates for a split-spread dataset,
we design the coordinates considering the direction of both the source and receiver waves at the surface.
|
|---|
|
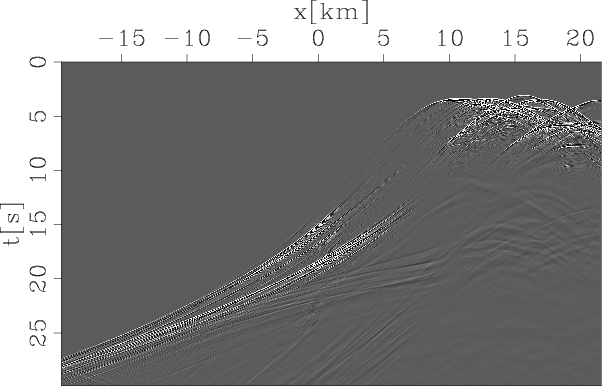
zigdata
Figure 8. The exploding reflector dataset from the revised Sigsbee 2A model. The overturned energy is recorded from |
|
|

|
|---|
|
zigimage
Figure 9. Migrated image of the overturned waves: migration in tilted coordinates (a) and reverse-time migration (b). |
|
|
|
|
|
|
Plane-wave migration in tilted coordinates |