Radon transform parameters

The performance of the Radon transform to focus the primaries and multiples to separate regions of the transformed domain, depends on the choice of curvature parameters and apex-shift values. In particular, curvatures should range from small negative values to allow for the possibility of slightly under-migrated primaries, to large enough values to accommodate the maximum curvatures of the over-migrated multiples. I have found that these are not particularly critical parameters as long as the curvature sampling is fine enough to avoid aliasing in the Radon domain. Similarly for the apex-shift parameters. They are not critical, since their role is only to provide room for the mapping of the diffracted multiples, thus preventing them from interfering with the primaries and the specular multiples that map to the zero apex-shift plane. A critical step is the design of the mute pattern to eliminate the primaries and keep the multiples. There are several ways that this could be implemented. I constructed a mask of ones for the multiple regions and zeros for the primary region, smoothed it laterally and in depth and multiplied it by the transformed data.

An important, and somewhat difficult parameter to estimate, is the one that controls the Cauchy regularization (parameter 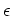$b$ in equation 33). We want the data in the ADCIG to be explained in the Radon domain by as few parameters as possible but avoiding the risk of attenuating the contribution from weak subsalt primaries. This is a trial and error parameter and it requires some testing to get a satisfactory value.