|
|
|
|
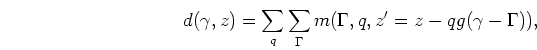 is the lateral apex shift (in units of aperture angle). In this way, I
transform the
two-dimensional data space of ADCIGs,
is the lateral apex shift (in units of aperture angle). In this way, I
transform the
two-dimensional data space of ADCIGs,
In the ideal case of migration with the correct velocity, primaries would be
perfectly horizontal in the ADCIGs
and would thus map in the model space to the zero-curvature (![]() ) plane,
) plane,
![]() , a plane of dimensions depth and apex-shift distance
, a plane of dimensions depth and apex-shift distance ![]() .
Specular multiples would map to the zero apex-shift distance
(
.
Specular multiples would map to the zero apex-shift distance
(![]() ) plane,
) plane, ![]() , a plane of dimensions depth and curvature
, a plane of dimensions depth and curvature ![]() .
Diffracted multiples would map elsewhere in the cube depending on
their curvature and apex-shift distance.
.
Diffracted multiples would map elsewhere in the cube depending on
their curvature and apex-shift distance.
|
|
|
|