 |
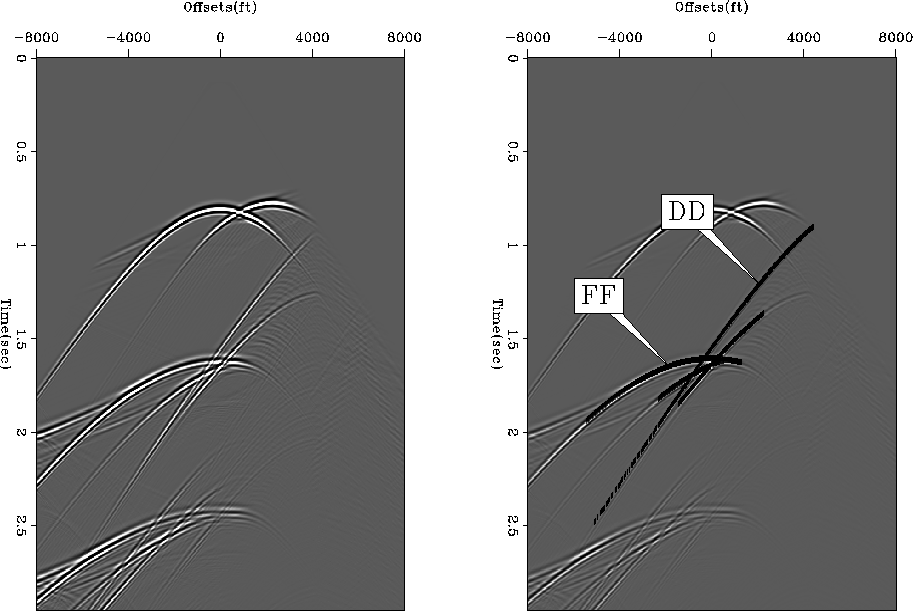
Figure 3 (a) A shot record corresponding to a shot located at a surface location of 5000. (b) Shot record with first order multiples modeled analytically overlaid on them
| Type | Ray-path | Name | |
| 1 | Both the bounces on the flat part | FF | |
| 2 | First bounce on the flat part and second on the dipping | FD | |
| 3 | First bounce on the dipping part and second on the flat | DF | |
| 4 | Both the bounces on the dipping part | DD |
 |
Equations 4 and 5 give the travel time and offset as a function of ![]() (take-off angle) for the event FF,
(take-off angle) for the event FF,
| |
(4) |
| |
(5) |
![\begin{eqnarray}
t(\theta)=\frac{1}{V}.\{\frac{2d}{\cos \theta} + \frac{(x_d + \...
...d + \frac{d}{\tan \alpha} - x_s - 2 d \tan \theta] + 2d\tan \theta\end{eqnarray}](img9.gif) |
(6) | |
| (7) |
| |
(8) |
| |
(9) |
![\begin{eqnarray}
t(\theta) &=& \frac{1}{V}.[x_d + \frac{d}{\tan \alpha} - x_s].\...
...a - \theta)}.\frac{\cos(\theta- \alpha)}{\cos(3 \alpha - \theta)}]\end{eqnarray}](img13.gif) |
||
| (10) |
![\begin{eqnarray}
h(\theta) &=& [x_d + \frac{d}{\tan \alpha} - x_s].\frac{\sin \a...
...a - \theta)}.\{\tan(2\alpha - \theta) + \tan(4 \alpha - \theta)\}]\end{eqnarray}](img14.gif) |
||
| (11) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b) are overlaid the first-order multiple events modeled using the above equations.
(b) are overlaid the first-order multiple events modeled using the above equations.