




Next: Asking a better question
Up: Application
Previous: Application
Figure 1 shows the relative phase velocity error, clipped at 1%, for a Taylor-coefficient, sixth-order in space,
second-order in time scheme for the 2D acoustic wave equation operating for the case 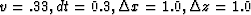 .The spatial stencil for this scheme occupies the central point and 3 points to the sides on each spatial axis.
I chose this particular combination of v and
.The spatial stencil for this scheme occupies the central point and 3 points to the sides on each spatial axis.
I chose this particular combination of v and 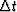 to simulate the situation where waves are propagating in the low-velocity
portion of a model that has a vmax:vmin ratio of 3:1.
This is where dispersion tends to be the greatest, so we want as much accuracy from our stencil as possible.
In some sense, models with a large vmax:vmin ratio are the most aggravating for
the finite-difference method.
Fine spatial sampling has to be used because of the low velocities,
but then really small time steps have to be used because of the high velocities.
As you might recall, accuracy tends to be better when you can run larger
time steps since the error from the time differencing will partially cancel the error from the spatial differences.
White areas of the wavenumber plane in Figure 1 have numerical phase velocities
less than .99 times the correct phase velocity.
Grey-colored areas have phase velocities within +/- 1% of the correct value, with neutral grey "perfect".
Black areas (which there are none in this figure), would be wavenumbers that have phase velocities more than 1% greater than the correct value.
This scheme is only accurate (to 1% anyway) out to about
45% of spatial Nyquist, requiring a sammple rate of about 4.4
points per shortest wavelength. This plot shows you the behavior of a finite-difference
scheme with Taylor-series derived coefficients quite well; excellent accuracy at zero wavenumber and a flatish
response out to some cutoff, then rapidly
increasing error.
to simulate the situation where waves are propagating in the low-velocity
portion of a model that has a vmax:vmin ratio of 3:1.
This is where dispersion tends to be the greatest, so we want as much accuracy from our stencil as possible.
In some sense, models with a large vmax:vmin ratio are the most aggravating for
the finite-difference method.
Fine spatial sampling has to be used because of the low velocities,
but then really small time steps have to be used because of the high velocities.
As you might recall, accuracy tends to be better when you can run larger
time steps since the error from the time differencing will partially cancel the error from the spatial differences.
White areas of the wavenumber plane in Figure 1 have numerical phase velocities
less than .99 times the correct phase velocity.
Grey-colored areas have phase velocities within +/- 1% of the correct value, with neutral grey "perfect".
Black areas (which there are none in this figure), would be wavenumbers that have phase velocities more than 1% greater than the correct value.
This scheme is only accurate (to 1% anyway) out to about
45% of spatial Nyquist, requiring a sammple rate of about 4.4
points per shortest wavelength. This plot shows you the behavior of a finite-difference
scheme with Taylor-series derived coefficients quite well; excellent accuracy at zero wavenumber and a flatish
response out to some cutoff, then rapidly
increasing error.
So, the hope is to use the optimization method described above to create a set of spatial differencing coefficients that will
push the 1% error cutoff (or whatever error cutoff you wish) to higher wavenumbers, which enables the scheme to propagate higher
frequencies on the same grid for the same cost.
Figure 2 shows the relative phase velocity error for just such an "optimized"
7 point second-difference operator that occupies the same stencil as the Taylor method shown in Figure 1,
for the same velocity, time-step and spatial sample rates.
The weight term used in the objective function (equation 4)
was 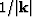 for
for 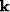 out to 80% of Nyquist with a superimposed taper down to
zero weight at 90% of Nyquist.
This is a pretty good illustration of "trying to do too much" and
least squares methods doing exactly what you told them to do, not necessarily
what you really want them to do.
It's probably important to state that the least squares method is not failing per se. Figure 3 shows a graph of the relative
phase velocity error along the kz axis and we can see the approximate "equiripple" behavior of the error,
typical of a least squares solution
over the wavenumber band we allowed in the
specification of the error function.
This behavior arises because the error at the high wavenumbers is naturally larger than at low wavenumbers.
With only a few coefficients,
there's no way to correct that error without compromising the behavior at low wavenumbers.
But in fact, if we were only going to propagate a short distance, this scheme has less
than 1% phase velocity error out to almost 80% of Nyquist.
out to 80% of Nyquist with a superimposed taper down to
zero weight at 90% of Nyquist.
This is a pretty good illustration of "trying to do too much" and
least squares methods doing exactly what you told them to do, not necessarily
what you really want them to do.
It's probably important to state that the least squares method is not failing per se. Figure 3 shows a graph of the relative
phase velocity error along the kz axis and we can see the approximate "equiripple" behavior of the error,
typical of a least squares solution
over the wavenumber band we allowed in the
specification of the error function.
This behavior arises because the error at the high wavenumbers is naturally larger than at low wavenumbers.
With only a few coefficients,
there's no way to correct that error without compromising the behavior at low wavenumbers.
But in fact, if we were only going to propagate a short distance, this scheme has less
than 1% phase velocity error out to almost 80% of Nyquist.





Next: Asking a better question
Up: Application
Previous: Application
Stanford Exploration Project
5/6/2007
![]() for
for ![]() out to 80% of Nyquist with a superimposed taper down to
zero weight at 90% of Nyquist.
This is a pretty good illustration of "trying to do too much" and
least squares methods doing exactly what you told them to do, not necessarily
what you really want them to do.
It's probably important to state that the least squares method is not failing per se. Figure 3 shows a graph of the relative
phase velocity error along the kz axis and we can see the approximate "equiripple" behavior of the error,
typical of a least squares solution
over the wavenumber band we allowed in the
specification of the error function.
This behavior arises because the error at the high wavenumbers is naturally larger than at low wavenumbers.
With only a few coefficients,
there's no way to correct that error without compromising the behavior at low wavenumbers.
But in fact, if we were only going to propagate a short distance, this scheme has less
than 1% phase velocity error out to almost 80% of Nyquist.
out to 80% of Nyquist with a superimposed taper down to
zero weight at 90% of Nyquist.
This is a pretty good illustration of "trying to do too much" and
least squares methods doing exactly what you told them to do, not necessarily
what you really want them to do.
It's probably important to state that the least squares method is not failing per se. Figure 3 shows a graph of the relative
phase velocity error along the kz axis and we can see the approximate "equiripple" behavior of the error,
typical of a least squares solution
over the wavenumber band we allowed in the
specification of the error function.
This behavior arises because the error at the high wavenumbers is naturally larger than at low wavenumbers.
With only a few coefficients,
there's no way to correct that error without compromising the behavior at low wavenumbers.
But in fact, if we were only going to propagate a short distance, this scheme has less
than 1% phase velocity error out to almost 80% of Nyquist.