




Next: FRACTURED RESERVOIRS AND CRACK-INFLUENCE
Up: Berryman: Aligned vertical fractures,
Previous: INTRODUCTION
Thomsen's weak anisotropy method (Thomsen, 1986), being an approximation
designed specifically for use in velocity analysis for exploration geophysics,
is clearly not exact. Approximations incorporated into the formulas
become most apparent for greater angles 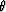 from the vertical, especially
for compressional and vertically polarized shear velocities
from the vertical, especially
for compressional and vertically polarized shear velocities
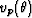 and
and 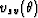 , respectively. Angle
, respectively. Angle 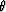 is
measured from the
is
measured from the 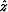 -vector pointing into the earth.
-vector pointing into the earth.
For reference purposes, we include here the exact velocity formulas for
P, SV, and SH seismic waves at all angles in a VTI elastic medium.
These results are available in many places (Rüger, 2002; Musgrave, 2003),
but were taken specifically from Berryman (1979)
with some minor changes of notation. The results are:
| ![\begin{displaymath}
v_p^2(\theta) = \frac{1}{2\rho}\left\{\left[\left(c_{11}+c_{...
...t(c_{33}+c_{44}\right)\cos^2\theta\right]
+ R(\theta)\right\}
\end{displaymath}](img5.gif) |
(1) |
and
| ![\begin{displaymath}
v_{sv}^2(\theta) = \frac{1}{2\rho}\left\{\left[\left(c_{11}+...
...(c_{33}+c_{44}\right)\cos^2\theta\right]
- R(\theta)\right\},
\end{displaymath}](img6.gif) |
(2) |
where
| ![\begin{displaymath}
R(\theta) = \sqrt{\left[\left(c_{11}-c_{44}\right)\sin^2\the...
...t]^2
+ 4\left(c_{13}+c_{44}\right)^2\sin^2\theta\cos^2\theta}
\end{displaymath}](img7.gif) |
(3) |
and, finally,
| ![\begin{displaymath}
v_{sh}^2(\theta) = \frac{1}{\rho}\left[c_{44}
+ (c_{66}-c_{44})\sin^2\theta\right].
\end{displaymath}](img8.gif) |
(4) |
Expressions for phase velocities in Thomsen's weak anisotropy
limit can be found in many places, including Thomsen (1986, 2002)
and Rüger (2002).
The pertinent expressions for phase velocities in VTI media as a function of angle 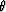 ,measured as before from the vertical direction, are
,measured as before from the vertical direction, are
| 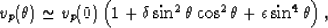 |
(5) |
| \sin^2\theta\cos^2\theta\right),
\end{displaymath}](img10.gif) |
(6) |
and
| 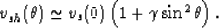 |
(7) |
In our present context, 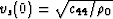 ,and
,and 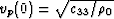 , where c33, c44, and
, where c33, c44, and 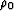 are two stiffnesses of the cracked medium and the mass density of the isotropic
host elastic medium. We assume that the cracks have insufficient volume
to affect the mass density
are two stiffnesses of the cracked medium and the mass density of the isotropic
host elastic medium. We assume that the cracks have insufficient volume
to affect the mass density 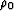 significantly.
significantly.
In each case, Thomsen's approximation has included a step that removes the
square on the left-hand side of the equation, by expanding a square root of the
right hand side. This step introduces a factor of 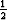 multiplying
the
multiplying
the 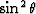 terms on the right hand side, and -- for example -- immediately
explains how equation (7) is obtained from (4).
The other two equations for
terms on the right hand side, and -- for example -- immediately
explains how equation (7) is obtained from (4).
The other two equations for 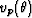 and
and 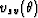 , i.e.,
(5) & (6), involve additional approximations as
well that we will not attempt to explain here.
, i.e.,
(5) & (6), involve additional approximations as
well that we will not attempt to explain here.
The three resulting Thomsen (1986) seismic parameters for weak anisotropy with
VTI symmetry are
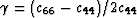 ,
,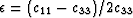 ,and
,and
| 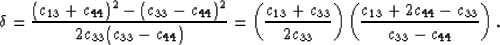 |
(8) |
All three of these parameters can play important roles in the velocities
given by (5)-(7) when the crack densities
are high enough. If crack densities are very low, then the SV shear wave will
actually have no dependence on angle of wave propagation. Note that the
so-called anellipticity parameter 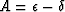 , vanishes
when
, vanishes
when 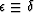 , which we will soon see does happen for low
crack densities.
, which we will soon see does happen for low
crack densities.





Next: FRACTURED RESERVOIRS AND CRACK-INFLUENCE
Up: Berryman: Aligned vertical fractures,
Previous: INTRODUCTION
Stanford Exploration Project
5/6/2007
![]() from the vertical, especially
for compressional and vertically polarized shear velocities
from the vertical, especially
for compressional and vertically polarized shear velocities
![]() and
and ![]() , respectively. Angle
, respectively. Angle ![]() is
measured from the
is
measured from the ![]() -vector pointing into the earth.
-vector pointing into the earth.
![]() ,measured as before from the vertical direction, are
,measured as before from the vertical direction, are
![]() multiplying
the
multiplying
the ![]() terms on the right hand side, and -- for example -- immediately
explains how equation (7) is obtained from (4).
The other two equations for
terms on the right hand side, and -- for example -- immediately
explains how equation (7) is obtained from (4).
The other two equations for ![]() and
and ![]() , i.e.,
(5) & (6), involve additional approximations as
well that we will not attempt to explain here.
, i.e.,
(5) & (6), involve additional approximations as
well that we will not attempt to explain here.
![]() ,
,![]() ,and
,and