Migration vs. "Hessian impulse response"

Another important comparison is the between the the one-way modeled data migration (Figures b and b) and the migration "Hessian impulse response" (Figures c and c). This two results should have been identical if all the off-diagonal terms of the Hessian matrix would have been computed (equation 7) to obtain Figures c. In the modeling of the one-way data all the off-diagonal elements of the Hessian matrix are implicitly computed. 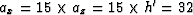To obtain Figure c only ($a_x=15\times a_z=15\times h'=32$) off-diagonal elements of the Hessian matrix were computed.

The two results are very similar at small offsets, but at far subsurface-offset the migration "Hessian impulse response" (Figure c) amplitudes are washed out. That might indicate the need of computing more off-diagonal coefficients in the (x,z) dimensions (a_x,a_z), probably the same number off subsurface-offsets. The angle migration "Hessian impulse response" differs at higher angles to the angle one-way modeled data migration, a result that is the consequence of the washed out amplitudes at far subsurface-offset "Hessian impulse response".

An important feature to notice when comparing Figures a, b, and c is that some places with low illumination in Figure a, have high illumination in Figure b, and Figure c. In those places the deconvolution by the one-way wave-equation Hessian will not recover the correct amplitudes. Thus the AVA signature will be affected.