Inversion

Deconvolution by the one-way wave-equation Hessian can be use to account for the illumination problem caused by the low velocity Gaussian anomaly (Figure ). To understand the effect of using one-way wave-equation Green functions in the Hessian computation, I compare the inversion of the: two-way modeled data (Figures a, and a), the one-way modeled data (Figures b, and b), and the migration "Hessian impulse response" (Figures c, and c). The images in Figure are the result of applying an offset to angle transformation to the images in Figure .

 

compare_inv1
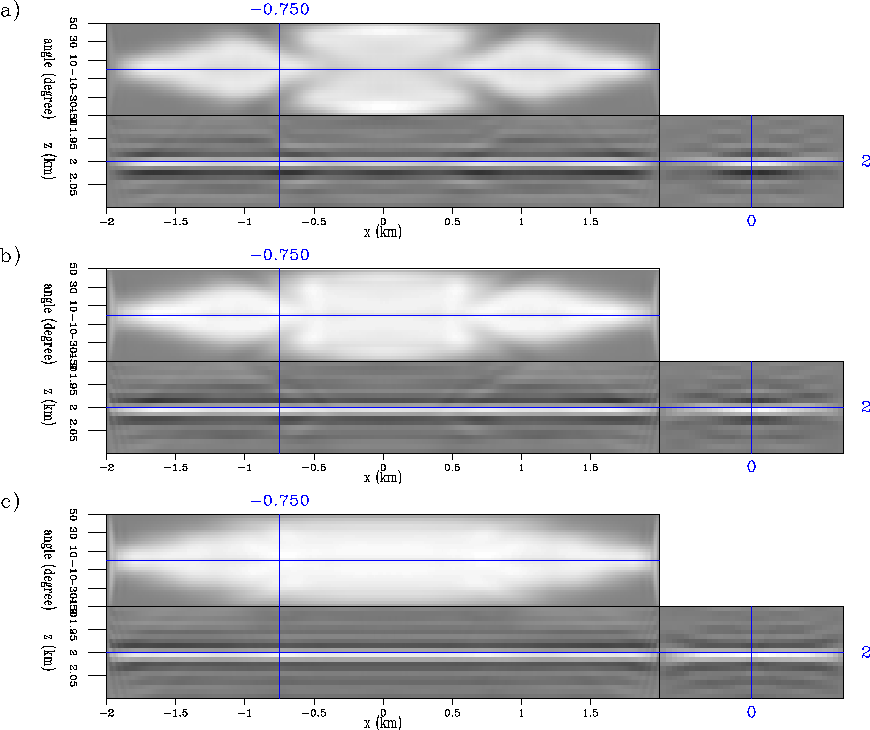
Figure 5 Comparison of the inversion results in reflection angle of the two-way (a) vs. the one-way modeled data (b), and vs. the migration "Hessian impulse response" (c) (from equation 3)

 

compare_inv4
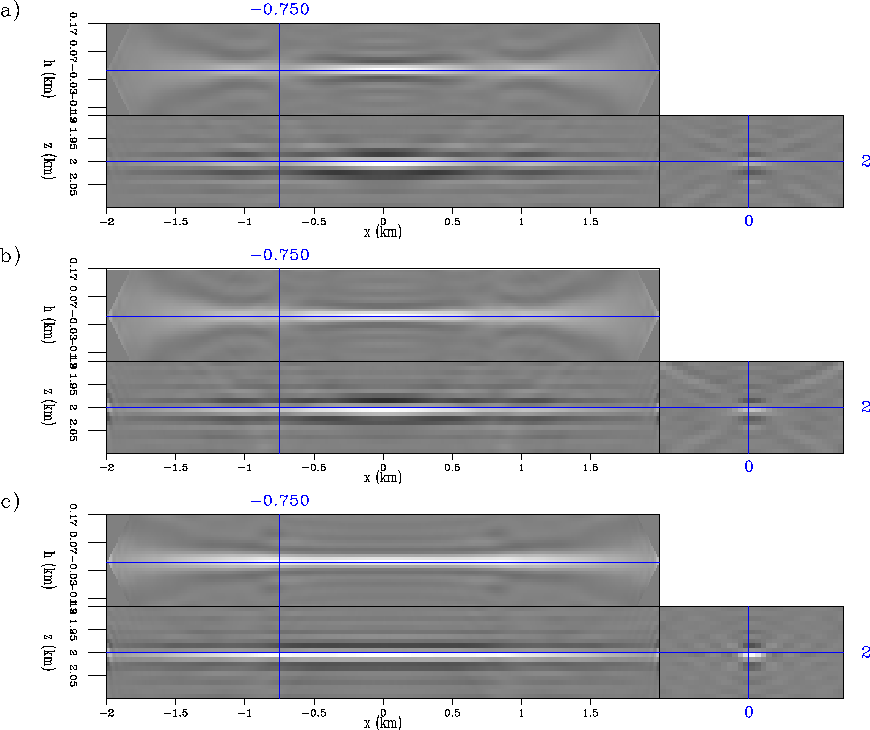
Figure 6 Comparison of the inversion results in reflection angle of the two-way (a) vs. the one-way modeled data (b), and vs. the migration "Hessian impulse response" (c) (from equation 3)

The first thing to notice is that in the case in that the same operator was used for the modeling and for the inversion ("Hessian impulse response", Figures c, and c) the deconvolution by the Hessian gives a almost perfect result. See how the energy in the subsurface-offset dimension concentrates around zero subsurface-offset (Figure c), and by consequence the more uniform angle coverage (Figure c) compare to the migration results in Figures c and c.

The second best result is obtained for the one-way modeled data inversion (Figures b, and b). Here the operators used for the modeling (implicitly) and the operator used for the inversion (explicitly) differ, since not all the of off-diagonal elements of the Hessian were computed. Nevertheless, there is an improvement in the AVA uniformity (expected from modeling) in most of the x positions. Especially at the center of the model.

The result of the two-way modeled data inversion (Figures a, and a) is the one showing less improvements. Nevertheless, there are several x positions where the AVA looks less affected by the velocity anomaly. Especially at the center of the model.

The results indicate that if the modeling and the inversion operators differ there is little chance to recover the correct AVA in poorly illuminated areas. This is because, in areas of poor illumination, this problem will have a large null space. The proper strategy appears to be the use of regularization. Three different regularization schemes for wave-equation inversion have been discussed in the literature. First, an identity operator (damping) which is customary in many scientific applications. Second, a geophysical regularization which penalizes the roughness of the image in the offset ray parameter dimension (which is equivalent the reflection angle dimension) Kuehl and Sacchi (2001); Prucha et al. (2000). Third, a differential semblance operator to penalize the energy in the image not focused at zero subsurface-offset Shen et al. (2003).